题目内容
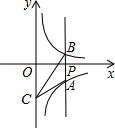 (2012•通辽)如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=-
(2012•通辽)如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=-| 6 |
| x |
| 4 |
| x |
分析:设P(a,0),由直线APB与y轴平行,得到A和B的横坐标都为a,将x=a代入反比例函数y=-
和y=
中,分别表示出A和B的纵坐标,进而由AP+BP表示出AB,三角形ABC的面积=
×AB×P的横坐标,求出即可.
| 6 |
| x |
| 4 |
| x |
| 1 |
| 2 |
解答:解:设P(a,0),a>0,则A和B的横坐标都为a,
将x=a代入反比例函数y=-
中得:y=-
,故A(a,-
);
将x=a代入反比例函数y=
中得:y=
,故B(a,
),
∴AB=AP+BP=
+
=
,
则S△ABC=
AB•xP的横坐标=
×
×a=5.
故选C
将x=a代入反比例函数y=-
| 6 |
| x |
| 6 |
| a |
| 6 |
| a |
将x=a代入反比例函数y=
| 4 |
| x |
| 4 |
| a |
| 4 |
| a |
∴AB=AP+BP=
| 6 |
| a |
| 4 |
| a |
| 10 |
| a |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| a |
故选C
点评:此题考查了反比例函数系数k的几何意义,以及坐标与图形性质,其中设出P的坐标,表示出AB是解本题的关键.

练习册系列答案
相关题目
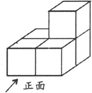 (2012•通辽)如图,有五个相同的小立方块搭成的几何体,这个几何体的左视图是( )
(2012•通辽)如图,有五个相同的小立方块搭成的几何体,这个几何体的左视图是( ) (2012•通辽)如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A′处,若∠A′BC=15°,则∠A′BD的度数为
(2012•通辽)如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A′处,若∠A′BC=15°,则∠A′BD的度数为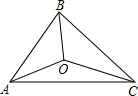 (2012•通辽)如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=
(2012•通辽)如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=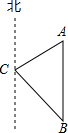 (2012•通辽)如图,小艳家(点A)在学校(点C)北偏东60°方向,AC=600(m).小颖家(点B)在小艳家正南,学校在小颖家北偏西45°方向.
(2012•通辽)如图,小艳家(点A)在学校(点C)北偏东60°方向,AC=600(m).小颖家(点B)在小艳家正南,学校在小颖家北偏西45°方向.