题目内容
(1998•内江)已知:如图,△ABC、△ABE内接于⊙O,AD是BC边上的高,且AC•BE=AE•CD求证:AE是⊙O的直径.
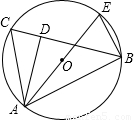
【答案】分析:要求证:AE是⊙O的直径,只要求证所对的圆周角是直角就可以,可以通过相似三角形证得(△ACD∽△AEB),得到∠ABE是直角即可证得AE是直径.
解答:证明:∵AC•BE=AE•CD,
∴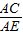 =
=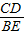 .
.
又∵∠C=∠E,
∴△ACD∽△AEB.
∴∠ADC=∠ABE.
∴∠ABE=90°.
∴AE是⊙O的直径.
点评:本题主要考查了90度的圆周角所对的弦是直径与相似三角形的判定与性质.
解答:证明:∵AC•BE=AE•CD,
∴
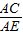 =
=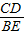 .
.又∵∠C=∠E,
∴△ACD∽△AEB.
∴∠ADC=∠ABE.
∴∠ABE=90°.
∴AE是⊙O的直径.
点评:本题主要考查了90度的圆周角所对的弦是直径与相似三角形的判定与性质.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
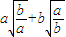 的值是 .
的值是 . ,则2x+1-|2x-1|可以化简为( )
,则2x+1-|2x-1|可以化简为( )