Question

(本题12分)如图，在平面直角坐标系中，点A（10，0），以OA为直径在第一象限内作半圆C，点B是该半圆周上一动点，连结OB、AB，并延长AB至点D，使DB=AB，过点D作x轴垂线，分别交x轴、直线OB于点E、F，点E为垂足，连结CF．
（1）当∠AOB=30°时，求弧AB的长度；
（2）当DE=8时，求线段EF的长；
（3）在点B运动过程中，是否存在以点E、C、F为顶点的三角形与△AOB相似，若存在，请求出此时点E的坐标；若不存在，请说明理由．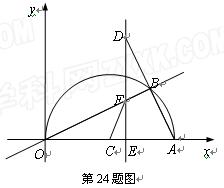

Answer 1

(本题12分)
（1）连结BC,
∵A（10，0）, ∴OA="10" ,CA=5,
∵∠AOB=30°,
∴∠ACB=2∠AOB=60°,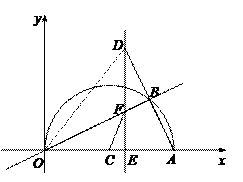
∴弧AB的长=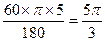;   ……4分
（2）连结OD,
∵OA是⊙C直径, ∴∠OBA=90°,
又∵AB=BD,
∴OB是AD的垂直平分线,
∴OD=OA=10,
在Rt△ODE中，
OE=,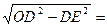
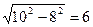∴AE=AO－OE=10-6=4,
由∠AOB=∠ADE=90°-∠OAB，∠OEF=∠DEA，
得△OEF∽△DEA,
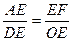∴,即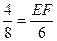，∴EF=3；……4分
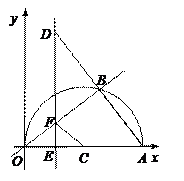（3）设OE=x，
①当交点E在O，C之间时，由以点E、C、F为顶点的三角
形与△AOB相似，有∠ECF=∠BOA或∠ECF=∠OAB，
当∠ECF=∠BOA时，此时△OCF为等腰三角形，点E为OC
中点，即OE=，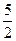
∴E₁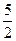（，0）；
当∠ECF=∠OAB时，有CE=5-x, AE=10-x，
∴CF∥AB,有CF=,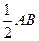
∵△ECF∽△EAD,
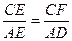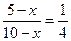∴,即,解得：,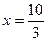
∴E₂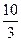（，0）;[来源:学科网ZXXK]
②当交点E在点C的右侧时，
∵∠ECF＞∠BOA，
∴要使△ECF与△BAO相似，只能使∠ECF=∠BAO，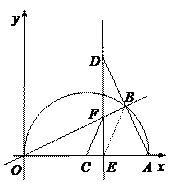
连结BE，
∵BE为Rt△ADE斜边上的中线，
∴BE=AB=BD,
∴∠BEA=∠BAO,
∴∠BEA=∠ECF,
∴CF∥BE,  ∴,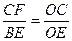
∵∠ECF=∠BAO, ∠FEC=∠DEA=Rt∠，
∴△CEF∽△AED, ∴,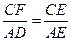
而AD=2BE,    ∴,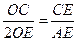
即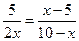, 解得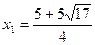, 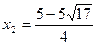＜0（舍去），
∴E₃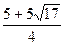（，0）;
③当交点E在点O的左侧时，
∵∠BOA=∠EOF＞∠ECF .
∴要使△ECF与△BAO相似，只能使∠ECF=∠BAO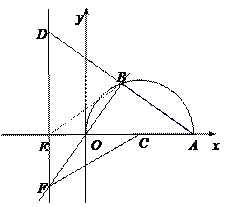
连结BE，得BE=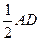=AB，∠BEA=∠BAO
∴∠ECF=∠BEA,
∴CF∥BE,
∴,
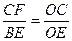又∵∠ECF=∠BAO, ∠FEC=∠DEA=Rt∠，
∴△CEF∽△AED, ∴，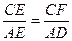
而AD=2BE,    ∴,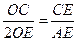
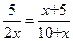∴,   解得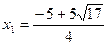, 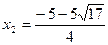＜0（舍去）,
∵点E在x轴负半轴上, ∴E₄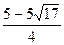（，0）,
综上所述：存在以点E、C、F为顶点的三角形与△AOB相似,此时点E坐标为：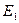
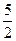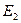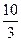（，0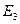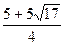）、（，0）、（，0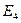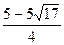）、（，0）．……4分

解析