ΧβΡΩΡΎ»ί
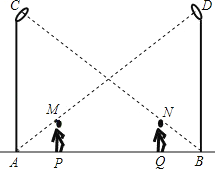
ΓΨΧβΡΩΓΩΡ≥ ΐ―ßΜνΕ·–ΓΉι‘Ύ“Μ¥ΈΜνΕ·÷–Θ§Ε‘“ΜΗω ΐΉ÷Έ ΧβΉς»γœ¬―–ΨΩΘΚ
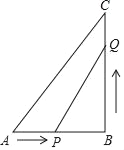
Θ®Έ ΧβΖΔœ÷Θ©»γΆΦΔΌΘ§‘ΎΒ»±Ώ»ΐΫ«–ΈABC÷–Θ§ΒψM «BC…œ»Έ“β“ΜΒψΘ§Ν§Ϋ”AMΘ§“‘AMΈΣ±ΏΉςΒ»±ΏΓςAMNΘ§Ν§Ϋ”CNΘ§≈–ΕœCNΚΆABΒΡΈΜ÷ΟΙΊœΒΘΚΓΓ ΓΓΘΜ
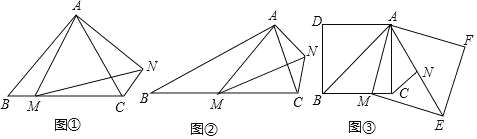
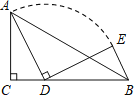
Θ®±δ ΫΧΫΨΩΘ©»γΆΦΔΎΘ§‘ΎΒ»―ϋ»ΐΫ«–ΈABC÷–Θ§BAΘΫBCΘ§ΒψM «BC±Ώ…œ»Έ“β“ΜΒψΘ®≤ΜΚ§ΕΥΒψBΘ§CΘ©Θ§Ν§Ϋ”AMΘ§“‘AMΈΣ±ΏΉςΒ»―ϋ»ΐΫ«–ΈAMNΘ§ ΙΕΞΫ«ΓœAMNΘΫΓœABCΘ§MAΘΫMNΘ§Ν§Ϋ”CNΘ§ ‘ΧΫΨΩΓœABC”κΓœACNΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…Θ°
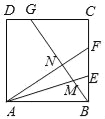
Θ®ΫβΨωΈ ΧβΘ©»γΆΦΔέΘ§‘Ύ’ΐΖΫ–ΈADBC÷–Θ§ΒψMΈΣBC±Ώ…œ“ΜΒψΘ§“‘AMΈΣ±ΏΉς’ΐΖΫ–ΈAMEFΘ§ΒψNΈΣ’ΐΖΫ–ΈAMEFΒΡ÷––ΡΘ§Ν§Ϋ”CNΘ§»τ’ΐΖΫ–ΈADBCΒΡ±Ώ≥ΛΈΣ8Θ§CNΘΫ![]() Θ§÷±Ϋ”–¥≥ω’ΐΖΫ–ΈAMEFΒΡ±Ώ≥ΛΘ°
Θ§÷±Ϋ”–¥≥ω’ΐΖΫ–ΈAMEFΒΡ±Ώ≥ΛΘ°
ΓΨ¥πΑΗΓΩΓΨΈ ΧβΖΔœ÷ΓΩ÷ΛΟςΦϊΫβΈωΘΜ
ΓΨ±δ ΫΧΫΨΩΓΩΓœABCΘΫΓœACNΘ§άμ”…ΦϊΫβΈωΘΜ
ΓΨΫβΨωΈ ΧβΓΩ’ΐΖΫ–ΈAMEFΒΡ±Ώ≥ΛΈΣ10Θ°
ΓΨΫβΈωΓΩ
ΓΨΈ ΧβΖΔœ÷ΓΩ
ΗυΨίΓςABCΘ§ΓςAMNΈΣΒ»±Ώ»ΐΫ«–ΈΘ§ΒΟΒΫAB=ACΘ§AM=AN«“ΓœBAC=ΓœMAN=60Γψ¥”ΕχΒΟΒΫΓœBAC-ΓœCAM=ΓœMAN-ΓœCAMΘ§Φ¥ΓœBAM=ΓœCANΘ§÷ΛΟςΓςBAMΓ’ΓςCANΘ§Φ¥Ω…ΒΟΒΫBM=CNΘ°
ΓΨ±δ ΫΧΫΨΩΓΩΗυΨίΓςABCΘ§ΓςAMNΈΣΒ»―ϋ»ΐΫ«–ΈΘ§ΒΟΒΫABΘΚBC=1ΘΚ1«“ΓœABC=ΓœAMNΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫ![]() Θ§άϊ”ΟΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœBAC=ΓœMANΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ§άϊ”ΟΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓœBAC=ΓœMANΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…ΒΟΒΫΫα¬έΘΜ
ΓΨΫβΨωΈ ΧβΓΩΗυΨί’ΐΖΫ–ΈΒΡ–‘÷ ΒΟΒΫΓœABC=ΓœBAC=45ΓψΘ§ΓœMAN=45ΓψΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ω![]() Θ§ΒΟΒΫBM=2Θ§CM=6Θ§‘ΌΗυΨίΙ¥Ι…Ε®άμΦ¥Ω…ΒΟΒΫ¥πΑΗΘ°
Θ§ΒΟΒΫBM=2Θ§CM=6Θ§‘ΌΗυΨίΙ¥Ι…Ε®άμΦ¥Ω…ΒΟΒΫ¥πΑΗΘ°
ΫβΘΚΓΨΈ ΧβΖΔœ÷ΓΩCNΓΈABΘ§
ΓΏΓςABC”κΓςMN «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύABΘΫACΘ§AMΘΫANΘ§ΓœBACΘΫΓœMANΘΫ60ΓψΘ§
ΓύΓœBAMΘΫΓœCANΘ§
‘ΎΓςABM”κΓςACN÷–Θ§ Θ§
Θ§
ΓύΓςABMΓ’ΓςACNΘ§
ΓύΓœBΘΫΓœACNΘΫ60ΓψΘ§
ΓΏΓœANC+ΓœACN+ΓœCANΘΫΓœANC+60Γψ+ΓœCANΘΫ180ΓψΘ§
ΓύΓœANC+ΓœMAN+ΓœBAMΘΫΓœANC+60Γψ+ΓœCANΘΫΓœBAN+ΓœANCΘΫ180ΓψΘ§
ΓύCNΓΈABΘΜ
ΓΨ±δ ΫΧΫΨΩΓΩ
ΓœABCΘΫΓœACNΘ§
άμ”…ΘΚΓΏ![]() ΘΫ1«“ΓœABCΘΫΓœAMNΘ§
ΘΫ1«“ΓœABCΘΫΓœAMNΘ§
ΓύΓςABCΓΪΓςAMNΘ§
Γύ![]() Θ§
Θ§
ΓΏABΘΫBCΘ§
ΓύΓœBACΘΫ![]() Θ§
Θ§
ΓΏAMΘΫMN
ΓύΓœMANΘΫ![]() Θ§
Θ§
ΓΏΓœBΘΫΓœAMNΘ§
ΓύΓœBAMΘΫΓœCANΘ§
ΓύΓςABMΓΪΓςACNΘ§
ΓύΓœABCΘΫΓœACNΘΜ
ΓΨΫβΨωΈ ΧβΓΩ
ΓΏΥΡ±Ώ–ΈADBCΘ§AMEFΈΣ’ΐΖΫ–ΈΘ§
ΓύΓœABCΘΫΓœBACΘΫ45ΓψΘ§ΓœMANΘΫ45ΓψΘ§
ΓύΓœBAC©¹ΓœMACΘΫΓœMAN©¹ΓœMAC
Φ¥ΓœBAMΘΫΓœCANΘ§
ΓΏ![]()
Γύ![]() Θ§
Θ§
ΓύΓςABMΓΪΓςACN
Γύ![]() Θ§
Θ§
Γύ![]()
Γύ![]() Θ§
Θ§
ΓύBMΘΫ2Θ§
ΓύCMΘΫ6
‘ΎRtΓςAMCΘ§ACΘΫ8Θ§CMΘΫ6Θ§
![]()
¥πΘΚ’ΐΖΫ–ΈAMEFΒΡ±Ώ≥ΛΈΣ10Θ°

 ΫΧ―ßΝΖ–¬Ά§≤ΫΝΖœΑœΒΝ–¥πΑΗ
ΫΧ―ßΝΖ–¬Ά§≤ΫΝΖœΑœΒΝ–¥πΑΗ ΩΈ«ΑΩΈΚσΆ§≤ΫΝΖœΑœΒΝ–¥πΑΗ
ΩΈ«ΑΩΈΚσΆ§≤ΫΝΖœΑœΒΝ–¥πΑΗ ΩΈΧΟ–ΓΉς“ΒœΒΝ–¥πΑΗ
ΩΈΧΟ–ΓΉς“ΒœΒΝ–¥πΑΗ ΜΤΗ‘–ΓΉ¥‘ΣΩΎΥψΥΌΥψΝΖœΑ≤αœΒΝ–¥πΑΗ
ΜΤΗ‘–ΓΉ¥‘ΣΩΎΥψΥΌΥψΝΖœΑ≤αœΒΝ–¥πΑΗ ≥…ΙΠ―ΒΝΖΦΤΜ°œΒΝ–¥πΑΗ
≥…ΙΠ―ΒΝΖΦΤΜ°œΒΝ–¥πΑΗ ±ΕΥΌ―ΒΝΖΖ®÷±Ά®÷–ΩΦΩΦΒψœΒΝ–¥πΑΗ
±ΕΥΌ―ΒΝΖΖ®÷±Ά®÷–ΩΦΩΦΒψœΒΝ–¥πΑΗ