题目内容
若二次函数y=x2-ax+1的图象与x轴无交点,则其图象可为下图中的
- A.

- B.
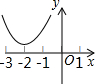
- C.
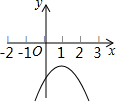
- D.

B
分析:由题意二次函数y=x2-ax+1的图象与x轴无交点,可得方程x2-ax+1=0的△<0,解得-2<a<2,再根据二次函数过点(0,1)来对A、B、C、D四个选项进行一一验证.
解答:已知二次函数解析式为:y=x2-ax+1
图象开口向上,
令x=0,得y=1,
∴二次函数图象过点(0,1)
∵二次函数y=x2-ax+1的图象与x轴无交点,
∴△=a2-4<0,
∴-2<a<2,
函数对称轴x=- >-1;
>-1;
∴只有B选项满足,
故选B.
点评:此题考查二次函数的基本性质及其图象,二次项系数与开口方向之间的关系,函数对称轴公式,考的知识点比较全面.
分析:由题意二次函数y=x2-ax+1的图象与x轴无交点,可得方程x2-ax+1=0的△<0,解得-2<a<2,再根据二次函数过点(0,1)来对A、B、C、D四个选项进行一一验证.
解答:已知二次函数解析式为:y=x2-ax+1
图象开口向上,
令x=0,得y=1,
∴二次函数图象过点(0,1)
∵二次函数y=x2-ax+1的图象与x轴无交点,
∴△=a2-4<0,
∴-2<a<2,
函数对称轴x=-
 >-1;
>-1;∴只有B选项满足,
故选B.
点评:此题考查二次函数的基本性质及其图象,二次项系数与开口方向之间的关系,函数对称轴公式,考的知识点比较全面.

练习册系列答案
相关题目
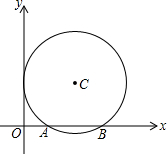 (2013•大庆)如图,平面直角坐标系中,以点C(2,
(2013•大庆)如图,平面直角坐标系中,以点C(2,