Question

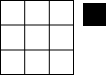
用边长为1的正方形覆盖3×3的正方形网格，最多覆盖边长为1的正方形网格（覆盖一部分就算覆盖）的个数是（　　）

• A、2
• B、4
• C、5
• D、6

Answer 1

分析：根据勾股定理可求得对角线的长，再根据覆盖一部分就算覆盖即可求得最多可覆盖的数量．

解答：解：根据勾股定理，得边长为1的正方形的对角线的长是

2

，把该正方形的对角线放在中间的正方形的任意一边上，因为

2

＞1，则根据题意，知该正方形最多可以覆盖6个正方形．
故选D．

点评：此题一要特别注意首先找到边长为1的正方形中的最长线段；二要注意理解题意，只要覆盖一部分就算覆盖．