题目内容
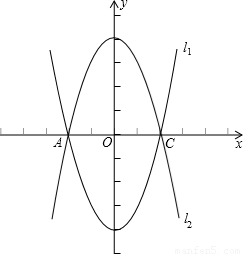
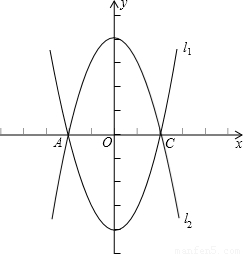
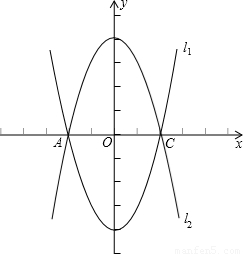
(2006•曲靖)如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点,(1)若抛物线l2与l1关于x轴对称,求l2的解析式;
(2)若点B是抛物线l1上的一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在l2上;
(3)探索:当点B分别位于l1在x轴上、下两部分的图象上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由.
【答案】分析:(1)因为关于x轴对称的点的特点是横坐标不变,纵坐标互为相反数,所以可得l2的解析式;
(2)设点B的坐标为(x1,x12-4),根据题意求的点D的坐标,代入解析式即可证明:点D在l2上;
(3)首先表示出S的值,根据函数值的范围即可得当点B在x轴上方时,y1>0,
S=4y1,它是关于y1的正比例函数且S随y1的增大而增大,∴S既无最大值也无最小值;
当点B在x轴下方时,-4≤y1<0,S最大=16.
解答:(1)解:设l2的解析式为y=a(x-h)2+k
∵l1与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),l1与l2关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4)(1分)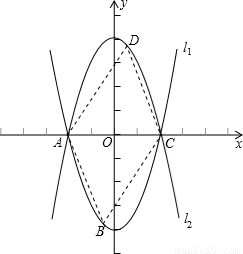
∴y=ax2+4(2分)
∴0=4a+4得a=-1
∴l2的解析式为y=-x2+4(3分)
(2)证明:设B(x1,y1)
∵点B在l1上
∴B(x1,x12-4)(4分)
∵四边形ABCD是平行四边形,A、C关于O对称
∴B、D关于O对称
∴D(-x1,-x12+4).(6分)
将D(-x1,-x12+4)的坐标代入l2:y=-x2+4
∴左边=右边
∴点D在l2上.(7分)
(3)解:设平行四边形ABCD的面积为S,
则S=2S△ABC=AC×|y1|=4|y1|
a.当点B在x轴上方时,y1>0
∴S=4y1,它是关于y1的正比例函数且S随y1的增大而增大,
∴S既无最大值也无最小值(8分)
b.当点B在x轴下方时,-4≤y1<0
∴S=-4y1,它是关于y1的正比例函数且S随y1的增大而减小,
∴当y1=-4时,S由最大值16,但他没有最小值
此时B(0,-4)在y轴上,它的对称点D也在y轴上.(9分)
∴AC⊥BD.
∴平行四边形ABCD是菱形(10分),
此时S最大=16.(11分)
点评:考查一次函数、二次函数的解析式、图象、性质等知识点,考查综合应用知识,分析问题解决问题的能力.
(2)设点B的坐标为(x1,x12-4),根据题意求的点D的坐标,代入解析式即可证明:点D在l2上;
(3)首先表示出S的值,根据函数值的范围即可得当点B在x轴上方时,y1>0,
S=4y1,它是关于y1的正比例函数且S随y1的增大而增大,∴S既无最大值也无最小值;
当点B在x轴下方时,-4≤y1<0,S最大=16.
解答:(1)解:设l2的解析式为y=a(x-h)2+k
∵l1与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),l1与l2关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4)(1分)

∴y=ax2+4(2分)
∴0=4a+4得a=-1
∴l2的解析式为y=-x2+4(3分)
(2)证明:设B(x1,y1)
∵点B在l1上
∴B(x1,x12-4)(4分)
∵四边形ABCD是平行四边形,A、C关于O对称
∴B、D关于O对称
∴D(-x1,-x12+4).(6分)
将D(-x1,-x12+4)的坐标代入l2:y=-x2+4
∴左边=右边
∴点D在l2上.(7分)
(3)解:设平行四边形ABCD的面积为S,
则S=2S△ABC=AC×|y1|=4|y1|
a.当点B在x轴上方时,y1>0
∴S=4y1,它是关于y1的正比例函数且S随y1的增大而增大,
∴S既无最大值也无最小值(8分)
b.当点B在x轴下方时,-4≤y1<0
∴S=-4y1,它是关于y1的正比例函数且S随y1的增大而减小,
∴当y1=-4时,S由最大值16,但他没有最小值
此时B(0,-4)在y轴上,它的对称点D也在y轴上.(9分)
∴AC⊥BD.
∴平行四边形ABCD是菱形(10分),
此时S最大=16.(11分)
点评:考查一次函数、二次函数的解析式、图象、性质等知识点,考查综合应用知识,分析问题解决问题的能力.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目