题目内容
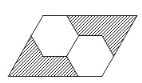
【题目】下列各图形都是由同样大小的圆和正三角形按一定的规律组成．其中，第①个图形由8个圆和1个正三角形组成，第②个图形由16个圆和4个正三角形组成，第③个图形由24个圆和9个正三角形组成，……则第_____个图形中圆和正三角形的个数相等 ．
【答案】8
【解析】
根据前面3个图形的关系可以推出第n个图形由（2n+1）×4-4=8n个圆和
个正三角形组成，代入可得结果
第①个图形由3×4-4=8个圆和1个正正三角形du组成，
第②个图形由5×4-4=16个圆和22=4个正三角形组成，
第③个图形由7×4-4=24个圆和32=9个正三角形组成，
…
所以第n个图形由（2n+1）×4-4=8n个圆和个正三角形组成，
∵圆和正三角形的个数相等，
∴8n=，
解得n=8，或n=0（不合题意，舍去）．
故答案是8
练习册系列答案
相关题目
【题目】某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动，每位同学必须且只能选择一项球类运动，对该校学生随机抽取
进行调查，根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
运动项目 | 频数(人数) |
羽毛球 | 30 |
篮球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |
请根据以上图表信息解答下列问题：
(1)频数分布表中的
，
；
(2)在扇形统计图中，“排球”所在的扇形的圆心角为 度；
(3)全校有多少名学生选择参加乒乓球运动？