题目内容
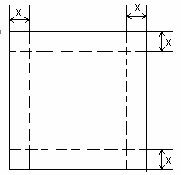
如图,一张边长为16厘米的正方形硬纸板,把它的四个角都剪去一个边长为x厘米的小正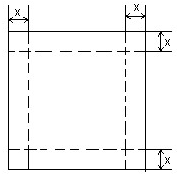 方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
(1)若用含有x的代数式表示V,则V=
(2)小明在做这个盒子时减去边长为3厘米的小正方形,小红在做这个盒子时减去边长为2厘米的小正方形,算算看,谁做的盒子容积大?
 方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:(1)若用含有x的代数式表示V,则V=
x(16-2x)2
x(16-2x)2
;(2)小明在做这个盒子时减去边长为3厘米的小正方形,小红在做这个盒子时减去边长为2厘米的小正方形,算算看,谁做的盒子容积大?
分析:(1)先根据已知条件表示出长方体底面边长,再乘以长方体的高即可;
(2)根据上面得出的关系式求当x=2、3时对应的V的值即可得出谁做的盒子容积大.
(2)根据上面得出的关系式求当x=2、3时对应的V的值即可得出谁做的盒子容积大.
解答:解:(1)一张边长为16cm的正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形后,
所形成的容器底面边长为16-2x,高为x,
则V=x(16-2x)2,
(2)在V=x(16-2x)2中,
当x=2时,V=2×(16-4)2=288,
当x=3时,V=3×(16-6)2=300,
小明做的盒子容积大.
故答案为:x(16-2x)2.
所形成的容器底面边长为16-2x,高为x,
则V=x(16-2x)2,
(2)在V=x(16-2x)2中,
当x=2时,V=2×(16-4)2=288,
当x=3时,V=3×(16-6)2=300,
小明做的盒子容积大.
故答案为:x(16-2x)2.
点评:此题考查了列代数式,关键是根据长方形面积和长方体的容积公式列出式子,计算时要细心.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
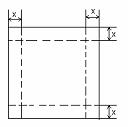
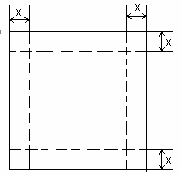
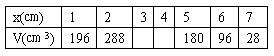
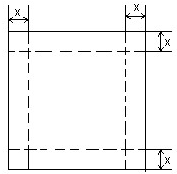
如图,一张边长为16㎝的正方形硬纸板,把它的四个角都剪去一个边长为x㎝的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为V㎝3,
请回答下列问题:
(1)若用含有X的代数式表示V,则V=
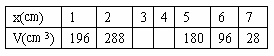
(2)完成下表:(4分)
| x(㎝) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V(㎝3) | 196 | 288 | 180 | 96 | 28 |
(3) 观察上表,容积V的值是否随x值得增大而增大?当x取什么值时,容积V的值最大?
 方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题: