题目内容
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
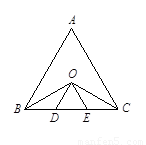
(1)试判定△ODE的形状,并说明你的理由.
(2)线段BD、DE、EC三者有什么关系?写出你理由.
(1)△ODE是等边三角形,证明见解析; (2)BD=DE=EC,证明见解析.
【解析】
试题分析:(1)直观上看△ODE是等边三角形,要证明一个三角形是等边三角形,要么证明三边相等,或者有两个角是60°或者有一个角是60°的等腰三角形,由题, 在等边△ABC中,AB=AC=BC, ∠ABC=∠ACB=60°,又∵OD∥AB,所以∠ABC=∠ODE=60°,同理, ∵OE∥AC,所以∠ACB=∠OED=60°,所以△ODE是等边三角形;(2)直观上看BD=DE=EC,∵∠ABC与∠ACB的平分线相交于点O,所以∠ABO=∠OBD, ∠ACO=∠OCD,又∵OD∥AB,所以∠OBD=∠ABO=∠BOD.所以BD=OD, ∵OE∥AC,所以∠ACO=∠OCD =∠COE,所以CE=OE,由(1)知△ODE是等边三角形,所以OD=DE=OE,即BD=DE=EC.
试题解析:(1)由题, 在等边△ABC中,AB=AC=BC, ∠ABC=∠ACB=60°,
又∵OD∥AB,
∴∠ABC=∠ODE=60°,
同理, ∵OE∥AC,
∴∠ACB=∠OED=60°,
∴△ODE是等边三角形.
(2)∵∠ABC与∠ACB的平分线相交于点O,
∴∠ABO=∠OBD, ∠ACO=∠OCD,
又∵OD∥AB,
∴∠OBD=∠ABO=∠BOD.
∴BD=OD,
∵OE∥AC,
∴∠ACO=∠OCD =∠COE,
∴CE=OE,
由(1)知△ODE是等边三角形,
∴OD=DE=OE,即BD=DE=EC.
考点:平行线的性质和等边三角形的判定.

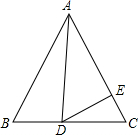 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
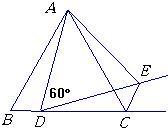 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是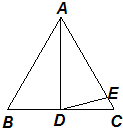 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.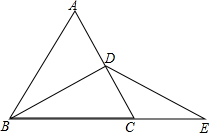 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: