Question

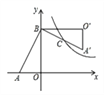
【题目】如图，在Rt△AOB中，两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，将△AOB绕点B逆时针旋转90°后得到△A′O′B．若反比例函数y=的图象恰好经过斜边A′B的中点C，S△ABO=16，tan∠BAO=2，则k的值为( )

A. 20 B. 22 C. 24 D. 26

Answer 1

【答案】C

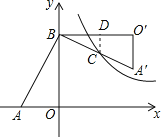
【解析】试题解析：设点C坐标为（x，y），作CD⊥BO′交边BO′于点D，

∵tan∠BAO=2，

∴，

∵S△ABO=AOBO=16，

∴AO=4，BO=8，

∵△ABO≌△A'O'B，

∴AO=A′O′=4，BO=BO′=8，

∵点C为斜边A′B的中点，CD⊥BO′，

∴CD=A′O′=2，BD=BO′=4，

∴x=BO-CD=8-2=6，y=BD=4，

∴k=xy=6×4=24．

故选C．