题目内容
初三（8）班尚剩班费m（m为小于400的整数）元，拟为每位同学买1本相册．某批发兼零售文具店规定：购相册50本起可按批发价出售，少于50本则按零售价出售，批发价比零售价每本便宜2元，班长若为每位同学买1本，刚好用完m元；但若多买12本给任课教师，可按批发价结算，也恰好只要m元．问该班有多少名同学？每本相册的零售价是多少元？
【答案】分析：设该班有x名同学，每本相册的零售价是y元，根据题意列出关于x、y的方程，再由x、y为整数即可求出x、y的可能值．
解答：解：设该班有x名同学，每本相册的零售价是y元，
则xy=（x+12）（y-2）①，且整数x满足38≤x＜50②，
由①得12y-2x-24=0，y=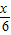
+2，xy=
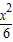+2x③，
由③及xy=m为整数，知整数x必为6的倍数，再由②得x只可能为42或48，
此时相应的y为9或10，
但m＜400，所以x=42，y=9．
故答案为：该班有42名同学，每本相册的零售价是9元．
点评：本题考查的是非一次不定方程，解答此类问题的关键是根据题意列出方程，再由x、y均为正整数的条件求解．
解答：解：设该班有x名同学，每本相册的零售价是y元，
则xy=（x+12）（y-2）①，且整数x满足38≤x＜50②，
由①得12y-2x-24=0，y=
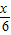+2，xy=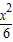+2x③，由③及xy=m为整数，知整数x必为6的倍数，再由②得x只可能为42或48，
此时相应的y为9或10，
但m＜400，所以x=42，y=9．
故答案为：该班有42名同学，每本相册的零售价是9元．
点评：本题考查的是非一次不定方程，解答此类问题的关键是根据题意列出方程，再由x、y均为正整数的条件求解．
练习册系列答案
相关题目