题目内容
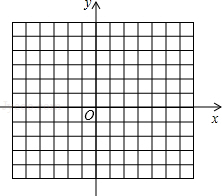
如图,△ABC三个顶点坐标分别为A(-4,2)B(-2,0),C(-4,0),且△A′B′C′与△ABC关于点P成位似,点A,C的对应点分别是A′(
,-1),C′(
,-1),
(1)画出位似中心点P;
(2)求出B点对应点B′点的坐标.
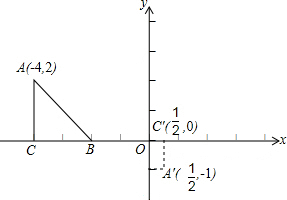
| 1 |
| 2 |
| 1 |
| 2 |
(1)画出位似中心点P;
(2)求出B点对应点B′点的坐标.
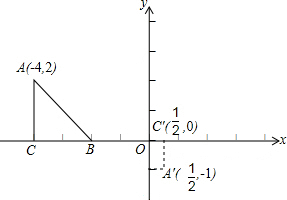
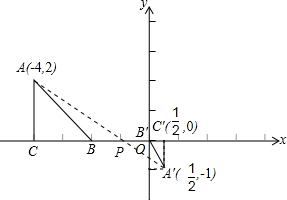
(1)由C与C′都在x轴上,故连接AA′,与x轴交于点P,则P为所求的位似中心;
(2)设直线AA′解析式为y=kx+b,
将A与A′坐标代入得:
,
解得:
,
则直线AA′解析式为y=-
x-
,
令y=0,解得:x=-1,
则P(-1,0),又B(-2,0),
则B′(0,0).
(2)设直线AA′解析式为y=kx+b,
将A与A′坐标代入得:
|
解得:
|
则直线AA′解析式为y=-
| 2 |
| 3 |
| 2 |
| 3 |
令y=0,解得:x=-1,
则P(-1,0),又B(-2,0),
则B′(0,0).


练习册系列答案
相关题目