题目内容
若关于x的函数y=(a-3)x2-(4a-1)x+4a的图象与坐标轴有两个交点,则a的值为( )
| A.3或0 | B.a>-
| ||||
C.0或-
| D.3或0或-
|
因为关于x的函数y=(a-3)x2-(4a-1)x+4a的图象与坐标轴只有两个交点,即与x轴、y轴各有一个交点.
所以此函数若为二次函数,则b2-4ac=[-(4a-1)]2-4(a-3)×4a=0,
即40a+1=0,
解得:a=-
;
若a=0,二次函数图象过原点,满足题意.
若此函数为一次函数,则a-3=0,所以a=3.
所以若关于x的函数y=(a-3)x2-(4a-1)x+4a的图象与坐标轴只有两个交点,则a=3或0或-
.
故选:D.
所以此函数若为二次函数,则b2-4ac=[-(4a-1)]2-4(a-3)×4a=0,
即40a+1=0,
解得:a=-
| 1 |
| 40 |
若a=0,二次函数图象过原点,满足题意.
若此函数为一次函数,则a-3=0,所以a=3.
所以若关于x的函数y=(a-3)x2-(4a-1)x+4a的图象与坐标轴只有两个交点,则a=3或0或-
| 1 |
| 40 |
故选:D.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目


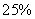 ,则本次捐款的中位数是( )元.
,则本次捐款的中位数是( )元.