题目内容
（2009•赤峰）如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC的度数是（ ）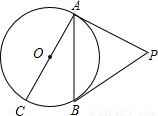
A．10°
B．20°
C．30°
D．40°
【答案】分析：连接BC，OB，根据圆周角定理先求出∠C，再求∠BAC．
解答：
解：连接BC，OB，
AC是直径，则∠ABC=90°，
PA、PB是⊙O的切线，A、B为切点，则∠OAP=∠OBP=90°，
∴∠AOB=180°-∠P=140°，
由圆周角定理知，∠C=
∠AOB=70°，
∴∠BAC=90°-∠C=20°．
故选B．
点评：本题利用了直径对的圆周角是直角，切线的概念，圆周角定理，四边形内角和定理求解．
解答：
解：连接BC，OB，AC是直径，则∠ABC=90°，
PA、PB是⊙O的切线，A、B为切点，则∠OAP=∠OBP=90°，
∴∠AOB=180°-∠P=140°，
由圆周角定理知，∠C=
∠AOB=70°，∴∠BAC=90°-∠C=20°．
故选B．
点评：本题利用了直径对的圆周角是直角，切线的概念，圆周角定理，四边形内角和定理求解．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
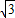），B（
，
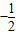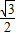），C（1，0），∠ABC=90°，BC与y轴的交点为D，D点坐标为（0，
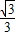），以点D为顶点y轴为对称轴的抛物线过点B．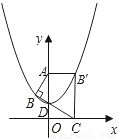
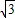），B（
，
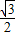），C（1，0），∠ABC=90°，BC与y轴的交点为D，D点坐标为（0，
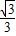），以点D为顶点y轴为对称轴的抛物线过点B．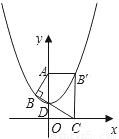
，0）沿y轴正方向平移1个单位长度得到点P，连接PO，再将PO绕点O按顺时针方向旋转120°，则PO在旋转过程中扫过的扇形面积为 ．（结果保留π）