题目内容
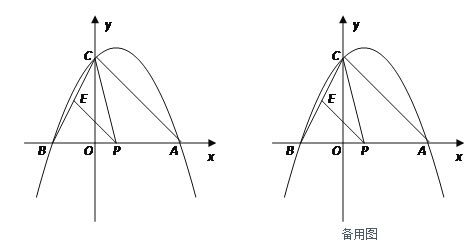
【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
【答案】(1)y=-0.5x2+x+4;(2)P(1,0);(3)存在,Q1(1,1),Q2(1, ![]() )Q3(1,-
)Q3(1,-![]() ),Q4(1,4+
),Q4(1,4+![]() ),Q5(1,4-
),Q5(1,4-![]() )
)
【解析】试题分析: (1)先通过解方程求出A,B两点的坐标,然后根据A,B,C三点的坐标,用待定系数法求出抛物线的解析式;(2)本题要通过求△CPE的面积与P点横坐标的函数关系式而后根据函数的性质来求△CPE的面积的最大值以及对应的P的坐标.△CPE的面积无法直接表示出,可用△CPB和△BEP的面积差来求,设出P点的坐标,即可表示出BP的长,可通过相似三角形△BEP和△BAC求出.△BEP中BP边上的高,然后根据三角形面积计算方法即可得出△CEP的面积,然后根据上面分析的步骤即可求出所求的值;(3)本题要分三种情况进行讨论:①QC=BC,那么Q点的纵坐标就是C点的纵坐标减去或加上BC的长.由此可得出Q点的坐标.②QB=BC,此时Q,C关于x轴对称,据此可求出Q点的坐标.③QB=QC,Q点在BC的垂直平分线上,可通过相似三角形来求出QC的长,进而求出Q点的坐标;
试题解析:
(1)∵x2-2x-8=0,
∴(x-4)(x+2)=0.
∴x1=4,x2=-2.
∴A(4,0),B(-2,0).
又∵抛物线经过点A、B、C,设抛物线解析式为y=ax2+bx+c(a≠0),
∴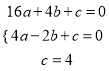
解得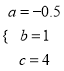
∴所求抛物线的解析式为y=-0.5x2+x+4;
(2)设P点坐标为(m,0),过点E作EG⊥x轴于点G,如图所示:
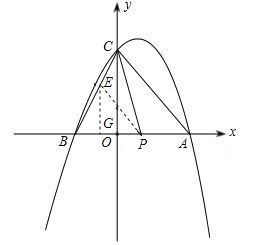
∵点B坐标为(-2,0),点A坐标(4,0),
∴AB=6,BP=m+2.
∵PE∥AC,
∴△BPE∽△BAC.
∴BP:AB=EG:CH
∴EG:4=(m+2):6
∴EG=(2m+4):3
∴S△CPE=S△CBP-S△EBP
=-1/3(m-1)2+3.
又∵-2≤m≤4,
∴当m=1时,S△CPE有最大值3.此时P点的坐标为(1,0);
(3)存在Q点,
∵BC=![]() ,
,
设Q(1,n),
当BQ=CQ时,
则32+n2=12+(n-4)2,
解得:n=1,
即Q1(1,1);
当BC=BQ=![]() ,时,9+n2=20,
,时,9+n2=20,
解得:n=±![]() ,
,
∴Q2(1, ![]() ),Q3(1,-
),Q3(1,-![]() );
);
当BC=CQ=![]() 时, ,1+(n-4)2=20,
时, ,1+(n-4)2=20,
解得:n=4±![]()
∴Q4(1,4+![]() ), Q5(1,4-
), Q5(1,4-![]() );
);
综上可得:坐标为Q1(1,1),Q2(1, ![]() )Q3(1,-
)Q3(1,-![]() ),Q4(1,4+
),Q4(1,4+![]() ),Q5(1,4-
),Q5(1,4-![]() ).
).
点睛: 本题着重考查了待定系数法求二次函数解析式、图形面积的求法、三角形相似、探究等腰三角形的构成情况等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

 阅读快车系列答案
阅读快车系列答案【题目】如图,锐角三角形ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,l与m相交于P点.若∠BAC=60°,∠ACP=24°,则∠ABP是( ) 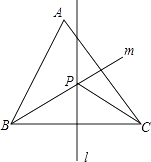
A.24°
B.30°
C.32°
D.36°
【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:

“限塑令”实施后,塑料购物袋使用后的处理方式统计表
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 总人数的百分比 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.