题目内容
【题目】如图，△ABC中，已知AB=AC，D是AC上的一点，CD=9，BC=15，BD=12．
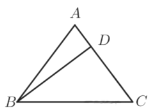
（1）判断△BCD的形状并证明你的结论．
（2）求△ABC的面积．
【答案】（1）见解析；（2）75
【解析】
（1）利用勾股定理的逆定理即可直接证明△BCD是直角三角形；
（2）设AD=x，则AC=x+9，在直角△ABD中，利用勾股定理即可列出方程，解方程，即可求解．
（1）∵CD=9，BD=12
∴CD2+BD2=81+144=225
∵BC=15
∴BC2=225
∴CD2+BD2=BC2
∴△BCD是直角三角形
（2）设AD=x，则AC=x+9
∵AB=AC
∴AB=x+9
∵∠BDC=90°
∴∠ADB=90°
∴AB2=AD2+BD2
即(x+9)2=x2+122
解得：x=
∴AC=+9=
∴S△ABC=
ACBD=
=75
故答案为：75
练习册系列答案
阅读快车系列答案
相关题目
