题目内容
计算题
小题1:
小题2:
小题3:12ab2(abc)4÷(-3a2b3c)÷[2(abc)3]
小题4:(a+b-c)(a-b+c)
小题1:

小题2:

小题3:12ab2(abc)4÷(-3a2b3c)÷[2(abc)3]
小题4:(a+b-c)(a-b+c)
小题1:原式=
 =
=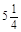
小题2:原式=
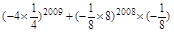 =
=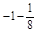 =-
=-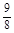
小题3:原式=12a5b6c4÷(-3a2b3c)÷[2a3b3c3]
=(-4a3b3c3)÷(2a3b3c3)
=-2
小题4:原式=[a+(b-c)][a-(b-c)]
=a2-(b-c)2
=a2-(b2-2bc+c2)
=a2-b2-c2+2bc
①先计算乘方和零指数幂,再进行有理数的加减混合运算;
②先运用积的乘方的逆运算,计算出乘方,再进行有理数的加减混合运算;
③先运用积的乘方计算,再运用整式的除法进行计算即可;
④先运用平方差公式,再运用完全平方公式,最后去括号即可.
解:①原式=6-1+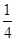 =5
=5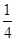
②原式=(-4×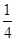 )2009+(-
)2009+(-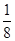 ×8)2008×(-
×8)2008×(-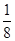 )=-1-
)=-1-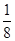 =-
=-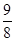 .
.
③原式=12a5b6c4÷(-3a2b3c)÷[2a3b3c3]
=(-4a3b3c3)÷(2a3b3c3)
=-2.
④原式=[a+(b-c)][a-(b-c)]
=a2-(b-c)2
=a2-(b2-2bc+c2)
=a2-b2-c2+2bc.
②先运用积的乘方的逆运算,计算出乘方,再进行有理数的加减混合运算;
③先运用积的乘方计算,再运用整式的除法进行计算即可;
④先运用平方差公式,再运用完全平方公式,最后去括号即可.
解:①原式=6-1+
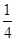 =5
=5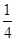
②原式=(-4×
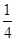 )2009+(-
)2009+(-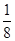 ×8)2008×(-
×8)2008×(-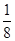 )=-1-
)=-1-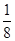 =-
=-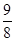 .
.③原式=12a5b6c4÷(-3a2b3c)÷[2a3b3c3]
=(-4a3b3c3)÷(2a3b3c3)
=-2.
④原式=[a+(b-c)][a-(b-c)]
=a2-(b-c)2
=a2-(b2-2bc+c2)
=a2-b2-c2+2bc.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
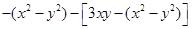 ,其中x=-1,y=2.
,其中x=-1,y=2. =0,化简代数式后求值:
=0,化简代数式后求值:
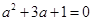 ,求
,求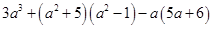 的值.
的值. -1都是整式
-1都是整式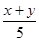 都是多项式
都是多项式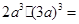 .
.