题目内容
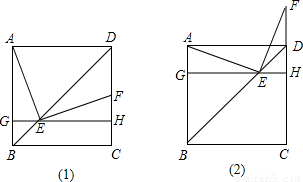
如图所示,已知E是边长为1的正方形ABCD对角线BD上一动点,点E从B点向D点运动(与B、D不重合),过点E作直线GH平行于BC,交AB于点G,交CD于点H,EF⊥AE于点E,交CD(或CD的延长线)于点F.(1)如图(1),求证:△AGE≌△EHF;
(2)点E在运动的过程中(图(1)、图(2)),四边形AFHG的面积是否发生变化?请说明理由.
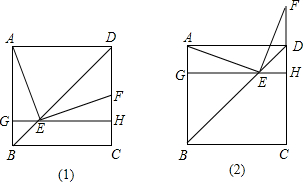
分析:(1)根据四边形ABCD是正方形,BD是对角线,且GH∥BC,求证△GEB和△HDE都是等腰直角三角形.又利用EF⊥AE
,可得∠EFH=∠AEG,然后即可求证△AGE≌△EHF.
(2)分两种情况进行讨论:(i)当点E运动到BD的中点时,利用四边形AFHG是矩形,可得S四边形AFHG=
(ii)当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形.由(1)知,△AGE≌△EHF,同理,图(2),△AGE≌△EHF可得,S四边形AFHG=
(FH+AG)•GH=
,然后即可得出结论.
,可得∠EFH=∠AEG,然后即可求证△AGE≌△EHF.
(2)分两种情况进行讨论:(i)当点E运动到BD的中点时,利用四边形AFHG是矩形,可得S四边形AFHG=
| 1 |
| 2 |
(ii)当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形.由(1)知,△AGE≌△EHF,同理,图(2),△AGE≌△EHF可得,S四边形AFHG=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵四边形ABCD是正方形,BD是对角线,且GH∥BC,
∴四边形AGHD和四边形GHCB都是矩形,
△GEB和△HDE都是等腰直角三角形.
∴∠AGE=∠EHF=90°,GH=BC=AB,EG=BG
∴GH-EG=AB-BG
即EH=AG
∴∠EFH+∠FEH=90°
又∵EF⊥AE,
∴∠AEG+∠FEH=90°.
∴∠EFH=∠AEG
∴△AGE≌△EHF
(2)四边形AFHG的面积没有发生变化.
(i)当点E运动到BD的中点时,
四边形AFHG是矩形,S四边形AFHG=
(ii)当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形.
由(1)知,△AGE≌△EHF
同理,图(2),△AGE≌△EHF
∴FH=EG=BG.
∴FH+AG=BG+AG=AB=1
这时,S四边形AFHG=
(FH+AG)•GH=
综合(i)、(ii)可知四边形AFHG的面积没有发生改变,都是
.
∴四边形AGHD和四边形GHCB都是矩形,
△GEB和△HDE都是等腰直角三角形.
∴∠AGE=∠EHF=90°,GH=BC=AB,EG=BG
∴GH-EG=AB-BG
即EH=AG
∴∠EFH+∠FEH=90°
又∵EF⊥AE,
∴∠AEG+∠FEH=90°.
∴∠EFH=∠AEG
∴△AGE≌△EHF
(2)四边形AFHG的面积没有发生变化.
(i)当点E运动到BD的中点时,
四边形AFHG是矩形,S四边形AFHG=
| 1 |
| 2 |
(ii)当点E不在BD的中点时,点E在运动(与点B、D不重合)的过程中,四边形AFHG是直角梯形.
由(1)知,△AGE≌△EHF
同理,图(2),△AGE≌△EHF
∴FH=EG=BG.
∴FH+AG=BG+AG=AB=1
这时,S四边形AFHG=
| 1 |
| 2 |
| 1 |
| 2 |
综合(i)、(ii)可知四边形AFHG的面积没有发生改变,都是
| 1 |
| 2 |
点评:此题主要考查正方形的性质,全等三角形的判定与性质等知识点的理解和掌握,此题有一定的拔高难度,属于难题.

练习册系列答案
相关题目
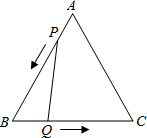 22、如图所示,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1m/s,点Q运动的速度是2m/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t s,解答下列问题:
22、如图所示,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,其中点P运动的速度是1m/s,点Q运动的速度是2m/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t s,解答下列问题: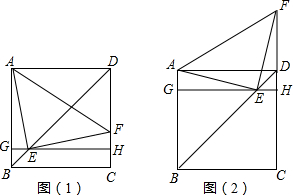 (2012•本溪二模)如图所示,已知E是边长为a的正方形ABCD对角线BD上一动点,点E从B点向D点运动(与B、D不重合),过点E作直线GH平行于BC,交AB于点G,交CD于点H,EF⊥AE于点E,交CD(或CD的延长线)于点F.
(2012•本溪二模)如图所示,已知E是边长为a的正方形ABCD对角线BD上一动点,点E从B点向D点运动(与B、D不重合),过点E作直线GH平行于BC,交AB于点G,交CD于点H,EF⊥AE于点E,交CD(或CD的延长线)于点F.