题目内容
关于x的方程ax2+bx+c=0的根为2和3,则方程ax2-bx-c=0的根
- A.-2,-3
- B.-6,1
- C.2,-3
- D.-1,6
B
分析:因为方程的两个根为2和3,所以方程可以方程因式为a(x-2)(x-3)=0,用含a的式子表示b和c,代入后面的方程可以用因式分解求出方程的根.
解答:∵ax2+bx+c=0的两根为2和3,
∴a(x-2)(x-3)=0,
整理得:ax2-5ax+6a=0,
∴b=-5a,c=6a.
把b,c代入方程ax2-bx-c=0,
得:ax2+5ax-6a=0,
a(x+6)(x-1)=0,
∴x1=-6,x2=1.
故选B.
点评:本题考查的是用因式分解法解一元二次方程,把方程的两根代入方程,整理后用含a的式子表示b和c,然后把b,c代入后面的方程,用因式分解法可以求出方程的根.
分析:因为方程的两个根为2和3,所以方程可以方程因式为a(x-2)(x-3)=0,用含a的式子表示b和c,代入后面的方程可以用因式分解求出方程的根.
解答:∵ax2+bx+c=0的两根为2和3,
∴a(x-2)(x-3)=0,
整理得:ax2-5ax+6a=0,
∴b=-5a,c=6a.
把b,c代入方程ax2-bx-c=0,
得:ax2+5ax-6a=0,
a(x+6)(x-1)=0,
∴x1=-6,x2=1.
故选B.
点评:本题考查的是用因式分解法解一元二次方程,把方程的两根代入方程,整理后用含a的式子表示b和c,然后把b,c代入后面的方程,用因式分解法可以求出方程的根.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2,且有x1-x1x2+x2=1-a,则a的值是( )
| A、1 | B、-1 | C、1或-1 | D、2 |
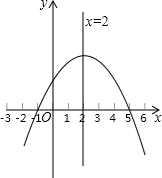 已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )
已知二次函数y=ax2+bx+c的图象如图所示,那么下列判断不正确的是( )| A、ac<0 | B、a-b+c>0 | C、b=-4a | D、关于x的方程ax2+bx+c=0的根是x1=-1,x2=5 |