题目内容
 已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.
已知在Rt△ABC中,∠C=90°,AD是∠BAC的角平分线,以AB上一点O为圆心,AD为弦作⊙O.(1)在图中作出⊙O(不写作法,保留作图痕迹),判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,tanB=
| 3 | 4 |
分析:(1)作线段AD的垂直平分线,交AB于O点,以O为圆心,OA为半径画圆即可.连接OD,由AD为角平分线可知∠OAD=∠CAD,由OA=OD可知∠OAD=∠ODA,得出内错角相等,判断OD∥AC即可;
(2)在Rt△ABC中,由AC=3,tanB=
,得BC=4,利用勾股定理得AB=5,设OA=OD=R,则OB=5-R,由△OBD∽△ABC,利用相似比求R的值.
(2)在Rt△ABC中,由AC=3,tanB=
| 3 |
| 4 |
解答: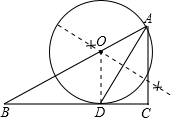 解:(1)直线BC与⊙O相切.理由如下:
解:(1)直线BC与⊙O相切.理由如下:
作图如图所示,连接OD,
∵AD为角平分线,∴∠OAD=∠CAD,
又∵OA=OD,∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC,
∵AC⊥BC,
∴OD⊥BC,
∴直线BC与⊙O相切;
(2)在Rt△ABC中,∵AC=3,tanB=
,
∴
=
,解得BC=4,由勾股定理,得AB=
=5,
设OA=OD=R,则OB=5-R,
∵∠ODB=∠ACB=90°,
∴OD∥AC,
∴△OBD∽△ABC,
∴
=
,即
=
,
解得R=
,∴⊙O的半径为
.
 解:(1)直线BC与⊙O相切.理由如下:
解:(1)直线BC与⊙O相切.理由如下:作图如图所示,连接OD,
∵AD为角平分线,∴∠OAD=∠CAD,
又∵OA=OD,∴∠OAD=∠ODA,
∴∠CAD=∠ODA,
∴OD∥AC,
∵AC⊥BC,
∴OD⊥BC,
∴直线BC与⊙O相切;
(2)在Rt△ABC中,∵AC=3,tanB=
| 3 |
| 4 |
∴
| AC |
| BC |
| 3 |
| 4 |
| AC2+BC2 |
设OA=OD=R,则OB=5-R,
∵∠ODB=∠ACB=90°,
∴OD∥AC,
∴△OBD∽△ABC,
∴
| OD |
| AC |
| OB |
| AB |
| R |
| 3 |
| 5-R |
| 5 |
解得R=
| 15 |
| 8 |
| 15 |
| 8 |
点评:本题考查了圆的作图,圆的切线的判定,相似三角形的判定与性质,解直角三角形是知识.关键是明确圆的有关性质,将圆的问题转化为三角形的问题进行解答.

练习册系列答案
相关题目
 如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( ) (1)已知在Rt△ABC中,∠C=90°,sinA=
(1)已知在Rt△ABC中,∠C=90°,sinA=