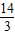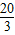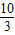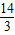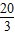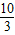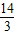题目内容
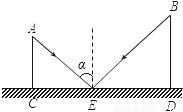
如图，CD是平面镜子，光线从A点射出，经CD上一点E反射后照射到B点，若入射角为α，AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，BD=6，CD=10，则线段ED的长为（ ）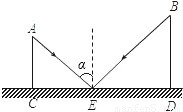
A．
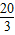
B．
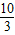
C．7
D．
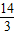
【答案】分析：根据镜面反射的性质可求出△ACE∽△BDE，再根据相似三角形的相似比解答即可．
解答：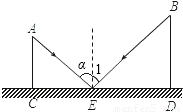
解：如图，
∵CD是平面镜，α为入射角，∠1为反射角
∴α=∠1．
∵α+∠AEC=90°，∠1+∠BED=90°
∴∠AEC=BED，
∵AC⊥CD，BD⊥CD
∴∠ACE=∠BDE=90°
∴Rt△ACE∽Rt△BDE，
∴
=
，
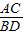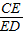∵AC=3，BD=6，CD=10
∴
=
，
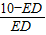解得ED=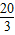
．
故选A．
点评：应用反射的基本性质，得出三角形相似，运用相似比即可解答．
解答：
解：如图，∵CD是平面镜，α为入射角，∠1为反射角
∴α=∠1．
∵α+∠AEC=90°，∠1+∠BED=90°
∴∠AEC=BED，
∵AC⊥CD，BD⊥CD
∴∠ACE=∠BDE=90°
∴Rt△ACE∽Rt△BDE，
∴
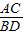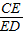=，∵AC=3，BD=6，CD=10
∴
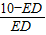=，解得ED=
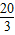．故选A．
点评：应用反射的基本性质，得出三角形相似，运用相似比即可解答．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
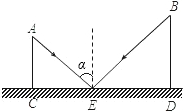如图，CD是平面镜子，光线从A点射出，经CD上一点E反射后照射到B点，若入射角为α，AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，BD=6，CD=10，则线段ED的长为（ ）A、
| ||
B、
| ||
| C、7 | ||
D、
|
如图，CD是平面镜子，光线从A点射出，经CD上一点E反射后照射到B点，若入射角为α，AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，BD=6，CD=10，则线段ED的长为（ ）
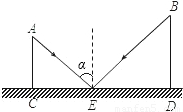
A．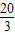
B．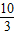
C．7
D．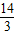
A．
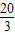
B．
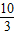
C．7
D．
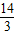
如图，CD是平面镜子，光线从A点射出，经CD上一点E反射后照射到B点，若入射角为α，AC⊥CD，BD⊥CD，垂足分别为C、D，且AC=3，BD=6，CD=10，则线段ED的长为（ ）
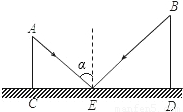
A．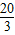
B．
C．7
D．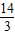
A．
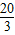
B．
C．7
D．
