题目内容
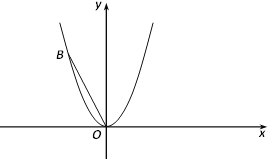
【题目】如图,平面直角坐标系xOy中,抛物线![]() 经过点B(-2,4).
经过点B(-2,4).
(1)求a的值;
(2)作Rt△OAB,使∠BOA=90°,且OB=2OA,求点A坐标;
(3)在(2)的条件下,过点A作直线AC⊥x轴于点C,交抛物线![]() 于点D,将该抛物线向左或向右平移t(t>0)个单位长度,记平移后点D的对应点为D′,点B的对应点为B′.当CD′+OB′的值最小时,请直接写出t的值和平移后相应的抛物线解析式.
于点D,将该抛物线向左或向右平移t(t>0)个单位长度,记平移后点D的对应点为D′,点B的对应点为B′.当CD′+OB′的值最小时,请直接写出t的值和平移后相应的抛物线解析式.
【答案】(1) ![]() .(2) (2,1)或(-2,-1).(3) t=1,
.(2) (2,1)或(-2,-1).(3) t=1, ![]() .
.
【解析】分析:(1)直接利用待定系数法求出抛物线解析式即可;(2)分两种情况讨论:点A在第一象限;点A在第三象限;(3)过点O作![]() 的平行线,再作点
的平行线,再作点![]() 关于x轴的对称点,利用勾股定理即可求解.
关于x轴的对称点,利用勾股定理即可求解.
(1)将点B(-2,4)代入y=ax (a≠0)得4a=4,∴a=1.
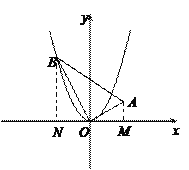
(2)如图①,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,
∴∠OMA=∠BNO=90°,∴∠NBO+∠NOB=90°.
∵∠BOA=90°,∴∠NOB+∠MOA=90°,
∴∠NBO=∠MOA,∴△BNO∽△OMA,
∴![]() .∵BN=4,NO=2,
.∵BN=4,NO=2,
∴OM=2,MA=1,
∴A点坐标为(2,1).
如图②,过点A作AM⊥y轴于点M,过点B作BN⊥y轴于点N,
同上可得OM=1,MA=2,
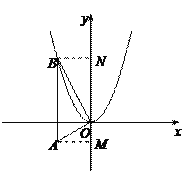
∴A点坐标为(-2,-1).
综上所述,A点坐标为(2,1)或(-2,-1).
(3)t=1, ![]() .
.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
