题目内容
(1997•广州)已知矩形ABCD的边AB=2,AB≠BC,矩形ABCD的面积为S,沿矩形的对称轴折叠一次得到一个新矩形,求这个新矩形的对角线的长度.
分析:先计算出AD=
,然后分类讨论:(1)如图1,折痕分别与AB、DC交于F、E点连结DF,根据折叠的性质得到AF=
AB=1,然后根据勾股定理可计算出DF;
(2)如图2,折痕分别与AD、BC交于E、F点,连结AF,根据折叠的性质得到BF=AE=
AD=
,然后根据勾股定理可计算出AF.
| S |
| 2 |
| 1 |
| 2 |
(2)如图2,折痕分别与AD、BC交于E、F点,连结AF,根据折叠的性质得到BF=AE=
| 1 |
| 2 |
| S |
| 4 |
解答:解:∵矩形ABCD的边AB=2,AB≠BC,矩形ABCD的面积为S,
∴AD=
,
(1)如图1,折痕分别与AB、DC交于F、E点,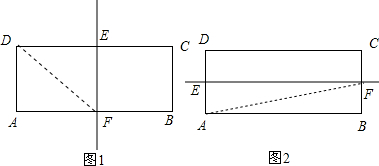 连结DF,
连结DF,
∵矩形ABCD沿直线EF对折,
∴AF=
AB=1,
∴DF=
=
=
,
即新矩形的对角线的长度为
;
(2)如图2,折痕分别与AD、BC交于E、F点,连结AF,
∵矩形ABCD沿直线EF对折,
∴BF=AE=
AD=
,
∴AF=
=
=
,
即新矩形的对角线的长度为
.
∴AD=
| S |
| 2 |
(1)如图1,折痕分别与AB、DC交于F、E点,
 连结DF,
连结DF,∵矩形ABCD沿直线EF对折,
∴AF=
| 1 |
| 2 |
∴DF=
| AD2+AF2 |
(
|
| 1 |
| 2 |
| S2+4 |
即新矩形的对角线的长度为
| 1 |
| 2 |
| S2+4 |
(2)如图2,折痕分别与AD、BC交于E、F点,连结AF,
∵矩形ABCD沿直线EF对折,
∴BF=AE=
| 1 |
| 2 |
| S |
| 4 |
∴AF=
| AB2+BF2 |
22+(
|
| 1 |
| 4 |
| S2+64 |
即新矩形的对角线的长度为
| 1 |
| 4 |
| S2+64 |
点评:本题考查折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等;对应点的连线段被折痕垂直平分.也考查了矩形的性质以及勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1997•广州)已知:线段a、b(如图)
(1997•广州)已知:线段a、b(如图)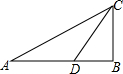 (1997•广州)已知:如图,△ABC中,∠C的平分线CD交AB于D,AD=5,CD=3,∠ADC=120°,求AC和BC:DB的值.
(1997•广州)已知:如图,△ABC中,∠C的平分线CD交AB于D,AD=5,CD=3,∠ADC=120°,求AC和BC:DB的值.