题目内容
【题目】如图,正方形ABCD与矩形EFGH在直线l的同侧,边AD,EH在直线l上,且AD=5cm,EH=4cm,EF=3cm.保持正方形ABCD不动,将矩形EFGH沿直线l左右移动,连接BF,CG,则BF+CG的最小值为_____________cm

【答案】![]()
【解析】
作点C关于FG的对称点P,连接GP,以FG,PG为邻边作平行四边形PGFQ,则BF+CG=BF+QF,当B,F,Q三点共线时,BF+CG的最小值为BQ的长,过点Q作QN⊥AB于N,依据勾股定理即可得到Rt△BNQ中,BQ=![]() ,即可得出BF+CG的最小值为
,即可得出BF+CG的最小值为![]() .
.
如图所示,作点C关于FG的对称点P,连接GP,
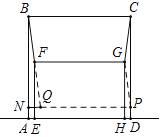
以FG,PG为邻边作平行四边形PGFQ,则FQ=PG=CG,FG=QP=4,
∴BF+CG=BF+QF,
∴当B,F,Q三点共线时,BF+CG的最小值为BQ的长,
过点Q作QN⊥AB于N,
由题可得BN=2(5-3)=4,NQ=5-4=1,
∴Rt△BNQ中,BQ=![]() ,
,
∴BF+CG的最小值为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某中学举行“汉字听写”比赛,每位学生听写汉字![]() 个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
组别 | 正确字数 | 人数 |
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
|


(1)在统计表中,![]() ,
,![]() ;
;
(2)补全条形统计图;
(3)在扇形统计图中“D组”所对应的圆心角的度数为 ;
(4)若该校共有![]() 名学生,如果听写正确的字数少于
名学生,如果听写正确的字数少于![]() 个定为不合格,请你估计这所中学这次比赛听写不合格的学生人数.
个定为不合格,请你估计这所中学这次比赛听写不合格的学生人数.