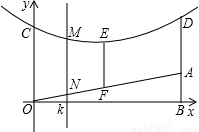
题目内容
在坡面为OA的斜坡上,有两根电线杆OC,AD,如图,以地平面为x轴,OC所在直线为 y轴,建立平面直角坐标系,已知OA=41米,AB=9米,OC=AD=10米,坡面中点F处与电线的距离EF=7.5米
y轴,建立平面直角坐标系,已知OA=41米,AB=9米,OC=AD=10米,坡面中点F处与电线的距离EF=7.5米(1)求电线所在的抛物线解析式;
(2)若平行于y轴的任意直线x=k交抛物线于点M,交坡面OA于点N,求MN的最小值.
分析:(1)由OA=41米,AB=9米,利用勾股定理求OB,确定C、D、E三点坐标,求抛物线解析式;
(2)求OA的解析式,则MN=抛物线解析式-直线OA解析式,再求MN的最小值.
(2)求OA的解析式,则MN=抛物线解析式-直线OA解析式,再求MN的最小值.
解答:解:(1)∵OA=41,AB=9,在Rt△OAB中,OB=
=40,
∴F(20,4.5),E(20,12),C(0,10),D(40,19),
设抛物线解析式为y=ax2+bx+c,则
,
解得
,
∴y=
x2-
x+10;
(2)∵A(40,9),
∴直线OA解析式为y=
x,
∴MN=(
x2-
x+10)-(
x)=
x2-
x+10=
(x-20)2+
,
∴MN的最小值为
米.
| OA2-AB2 |
∴F(20,4.5),E(20,12),C(0,10),D(40,19),
设抛物线解析式为y=ax2+bx+c,则
|
解得
|
∴y=
| 1 |
| 160 |
| 1 |
| 40 |
(2)∵A(40,9),
∴直线OA解析式为y=
| 9 |
| 40 |
∴MN=(
| 1 |
| 160 |
| 1 |
| 40 |
| 9 |
| 40 |
| 1 |
| 160 |
| 1 |
| 4 |
| 1 |
| 160 |
| 15 |
| 2 |
∴MN的最小值为
| 15 |
| 2 |
点评:本题考查了二次函数的运用.关键是根据题意,表示抛物线上的三点坐标,求抛物线解析式,运用二次函数的性质解题.

练习册系列答案
相关题目
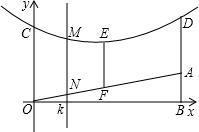 y轴,建立平面直角坐标系,已知OA=41米,AB=9米,OC=AD=10米,坡面中点F处与电线的距离EF=7.5米
y轴,建立平面直角坐标系,已知OA=41米,AB=9米,OC=AD=10米,坡面中点F处与电线的距离EF=7.5米