题目内容
设袋中有10个球,其中4个红球,4个白球,2个黑球,每个球除了颜色外都相同,从中随意取出1球,设P1=P(不是红球),P2=P(不是白球),P3=P(不是黑球),则P1、P2、P3的大小关系为( )A.P1<P2<P3
B.P1>P2>P3
C.P1=P2<P3
D.P1=P2>P3
【答案】分析:要求概率的大小,只需求出各自所占的比例大小即可.求比例时,应注意记清各自的数目.
解答:解:P1=P(不是红球)= ;
;
P2=P(不是白球)=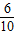 ;
;
P3=P(不是黑球)= .故P1=P2<P3
.故P1=P2<P3
故选C.
点评:用到的知识点为:概率=所求情况数与总情况数之比.
解答:解:P1=P(不是红球)=
 ;
;P2=P(不是白球)=
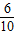 ;
;P3=P(不是黑球)=
 .故P1=P2<P3
.故P1=P2<P3故选C.
点评:用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设袋中有10个球,其中4个红球,4个白球,2个黑球,每个球除了颜色外都相同,从中随意取出1球,设P1=P(不是红球),P2=P(不是白球),P3=P(不是黑球),则P1、P2、P3的大小关系为( )
| A、P1<P2<P3 | B、P1>P2>P3 | C、P1=P2<P3 | D、P1=P2>P3 |