题目内容
三个同学对问题“若关于x、y的方程组
的解是
,求方程组
的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替代的方法来解决”.
(1)参考上面他们的讨论,请写出解答过程.
(2)利用上面的讨论方法,解方程:
.
|
|
|
(1)参考上面他们的讨论,请写出解答过程.
(2)利用上面的讨论方法,解方程:
|
分析:(1)所求方程组两方程两边除以5变形后,类比已知方程组的解列出方程组,求出方程组的解即可得到x与y的值;
(2)方程组变形后,类比即可求出x与y的值,得到方程组的解.
(2)方程组变形后,类比即可求出x与y的值,得到方程组的解.
解答:(1)
,
方程组两边除以5得:
,
∵方程组
的解是
,即
,
∴
,
解得:
;
(2)
,
变形得:
,
∴
,
解得
.
|
方程组两边除以5得:
|
∵方程组
|
|
|
∴
|
解得:
|
(2)
|
变形得:
|
∴
|
解得
|
点评:此题考查了二元一次方程组的解,以及解二元一次方程组,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
相关题目
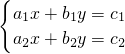 的解是
的解是 ,求方程组
,求方程组 的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替代的方法来解决”.
的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替代的方法来解决”. .
.