题目内容
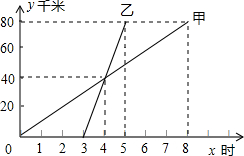 甲、乙两人分别骑自行车和摩托车从甲地到乙地
甲、乙两人分别骑自行车和摩托车从甲地到乙地(1)谁出发较早,早多长时间?谁到达乙地早?早多长时间?
(2)两人行驶速度分别是多少?
(3)分别求出自行车和摩托车行驶过程的函数解析式.
分析:(1)根据两条直线与x轴相交来判断谁先出发及出发时间,与y=80虚线相交判断谁先达到及到达时间;
(2)行驶速度=
;
(3)找出两点代入假定解析式求解析式.
(2)行驶速度=
| 距离 |
| 时间 |
(3)找出两点代入假定解析式求解析式.
解答:解:(1)甲出发较早,早3小时;乙到达乙地早,甲到达8小时,乙到达5小时,乙比甲早到3小时;
(2)甲行驶速度为
=10(千米/小时),
乙行驶速度为
=40(千米/小时);
(3)设自行车的函数解析式为:y=kx+b.将原点(0,0)和(4,40)代入解得y=10x;
设摩托车的函数解析式为:y=kx+b.将点(3,0)和(4,40)代入解得y=40x-120.
(2)甲行驶速度为
| 80 |
| 8 |
乙行驶速度为
| 80 |
| 2 |
(3)设自行车的函数解析式为:y=kx+b.将原点(0,0)和(4,40)代入解得y=10x;
设摩托车的函数解析式为:y=kx+b.将点(3,0)和(4,40)代入解得y=40x-120.
点评:此题为一次函数的应用,渗透了函数与方程的思想.

练习册系列答案
相关题目



