题目内容
 探究证明:
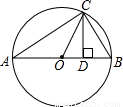
探究证明:如图,△ABC为⊙O的内接三角形,AB为直径,过点C作CD⊥AB于点D,设AD=a.BD=b.
(1)分别a,b表示线段OC,CD;
(2)探求OC与CD表达式之间存在的数量关系.(用含a,b的式子表示).
归纳结论:
根据上面的观察计算、探究证明,你能得
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
实践应用:
要制作面积为1平方米的长方形镜框,直接利用探究得出的结论,求出镜框周长的最小值.
分析:(1)求出∠ADC=∠BDC=90°,∠CAB=∠BCD,证△ADC∽△CDB,得出
=
,代入即可求出CD,求出AB,即可求出OC;
(2)分为两种情况:当O和D不重合时得出
>
,当O和D重合时得出
=
,即可得出答案;设长方形镜框ABCD的长AD=a,宽AB=b,根据面积求出
=1,根据
≥
,求出a+b≥2,得出2(a+b)≥4,求出2(a+b)的最小值即可.
| CD |
| DB |
| AD |
| CD |
(2)分为两种情况:当O和D不重合时得出
| a+b |
| 2 |
| ab |
| a+b |
| 2 |
| ab |
| ab |
| a+b |
| 2 |
| ab |
解答: 探究证明:
探究证明:
解:(1)∵AB为直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠CBA+∠BCD=90°,∠CBA+∠CAB=90°,
∴∠CAB=∠BCD,
∴△ADC∽△CDB,
∴
=
,
即
=
,
CD=
,
∵AB=AD+BD=a+b,
AB是⊙O直径,
∴半径OC=
AB=
;
即OC=
,CD=
;
(2)∵当D和O不重合时,如图,在Rt△OCD中,OC>CD,即
>
;
当D和O重合时,OC=CD,即
=
,
∴OC与CD表达式之间存在的数量关系是
≥
;
故答案为:
≥
.
实践应用:
解: 设长方形镜框ABCD的长AD=a,宽AB=b,
设长方形镜框ABCD的长AD=a,宽AB=b,
∵长方形镜框ABCD的面积是1平方米,
∴AB=CD=b,AD=BC=a,ab=1,
∴
=1,
∵由以上结论可知:
≥
,
∴
≥1,
即a+b≥2,
∴2(a+b)≥4,
即2(a+b)的最小值是4,
∵长方形镜框ABCD的周长是AB+BC+CD+AD=2a+2b=2(a+b),
∴镜框周长的最小值是4.
 探究证明:
探究证明:解:(1)∵AB为直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠CBA+∠BCD=90°,∠CBA+∠CAB=90°,
∴∠CAB=∠BCD,
∴△ADC∽△CDB,
∴
| CD |
| DB |
| AD |
| CD |
即
| CD |
| b |
| a |
| CD |
CD=
| ab |
∵AB=AD+BD=a+b,
AB是⊙O直径,
∴半径OC=
| 1 |
| 2 |
| a+b |
| 2 |
即OC=
| a+b |
| 2 |
| ab |
(2)∵当D和O不重合时,如图,在Rt△OCD中,OC>CD,即
| a+b |
| 2 |
| ab |
当D和O重合时,OC=CD,即
| a+b |
| 2 |
| ab |
∴OC与CD表达式之间存在的数量关系是
| a+b |
| 2 |
| ab |
故答案为:
| a+b |
| 2 |
| ab |
实践应用:
解:
 设长方形镜框ABCD的长AD=a,宽AB=b,
设长方形镜框ABCD的长AD=a,宽AB=b,∵长方形镜框ABCD的面积是1平方米,
∴AB=CD=b,AD=BC=a,ab=1,
∴
| ab |
∵由以上结论可知:
| a+b |
| 2 |
| ab |
∴
| a+b |
| 2 |
即a+b≥2,
∴2(a+b)≥4,
即2(a+b)的最小值是4,
∵长方形镜框ABCD的周长是AB+BC+CD+AD=2a+2b=2(a+b),
∴镜框周长的最小值是4.
点评:本题考查了勾股定理和相似三角形的性质和判定的应用,主要考查学生的理解能力和计算能力,能根据求出的结果得出规律是解此题的关键.

练习册系列答案
相关题目
 ,
, 时,
时,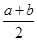 与
与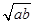 的大小关系是_________________.
的大小关系是_________________.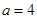 ,
,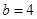 时,
时,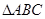 为圆O的内接三角形,
为圆O的内接三角形,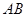 为直径,过C作
为直径,过C作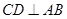 于D,设
于D,设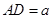 ,BD=b.
,BD=b.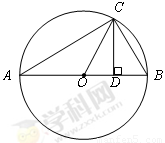
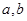 表示线段OC,CD;
表示线段OC,CD;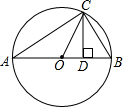 探究证明:
探究证明: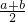 与
与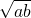 的大小关系是________.
的大小关系是________.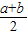 与
与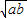 的大小关系是______
的大小关系是______