题目内容
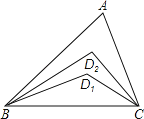
【题目】如图,在△ABC中,∠A=52°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是( )
A. 56° B. 60° C. 68° D. 94°
【答案】A
【解析】根据角平分线的性质和三角形的内角和定理可得.
∵∠A=52°,∴∠ABC+∠ACB=180°-52°=128°,
又∠ABC与∠ACB的角平分线交于D1,
∴∠ABD1=∠CBD1=![]() ∠ABC,∠ACD1=∠BCD1=
∠ABC,∠ACD1=∠BCD1=![]() ∠ACB,
∠ACB,
∴∠CBD1+∠BCD1=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×128°=64°,
×128°=64°,
∴∠BD1C=180°-![]() (∠ABC+∠ACB)=180°-64°=116°,
(∠ABC+∠ACB)=180°-64°=116°,
同理∠BD2C=180°-![]() (∠ABC+∠ACB)=180°-96°=84°,
(∠ABC+∠ACB)=180°-96°=84°,
依次类推,∠BD5C=180°-![]() (∠ABC+∠ACB)=180°-124°=56°.
(∠ABC+∠ACB)=180°-124°=56°.
故选A.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

