题目内容
若直线y=kx+2k+1与直线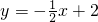
的交点在第一象限，则k的取值范围是
- A.
＜k＜
- B.
＜k＜ - C.k＞
- D.k＞
B
分析：求出两直线的交点坐标，根据交点在第一象限这一条件来确定k的取值范围．
解答：两直线的交点是：
，
解方程组得：
，
∵直线y=kx+2k+1与直线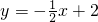的交点在第一象限，
∴
，
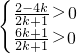解不等式组得：＜k＜，
故选B．
点评：解答本题的关键是列对二元一次方程组与一元一次不等式组．
分析：求出两直线的交点坐标，根据交点在第一象限这一条件来确定k的取值范围．
解答：两直线的交点是：
，解方程组得：
，∵直线y=kx+2k+1与直线
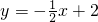的交点在第一象限，∴
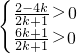，解不等式组得：
＜k＜，故选B．
点评：解答本题的关键是列对二元一次方程组与一元一次不等式组．
练习册系列答案
名校课堂系列答案
相关题目
若直线y=kx+2k+1与直线y=-
x+2的交点在第一象限，则k的取值范围是（ ）
| 1 |
| 2 |
A、-
| ||||
B、-
| ||||
C、k＞
| ||||
D、k＞-
|
如图．直线AB分别交y轴，x轴于A，B两点，已知A（0，2