题目内容
【题目】在平面直角坐标系中,已知线段![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,如图1所示.
,如图1所示.
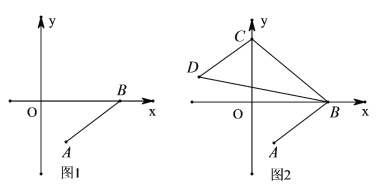
(1)平移线段![]()
![]() 到线段
到线段![]()
![]() ,使点
,使点![]() 的对应点为,点
的对应点为,点![]() 的对应点为
的对应点为![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)平移线段![]()
![]() 到线段
到线段![]()
![]() ,使点
,使点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在第二象限内(
在第二象限内(![]() 与
与![]() 对应,
对应, ![]() 与
与![]() 对应),连接
对应),连接![]() 如图2所示.若
如图2所示.若![]() 表示△BCD的面积),求点
表示△BCD的面积),求点![]() 、
、![]() 的坐标;
的坐标;
(3)在(2)的条件下,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,
的坐标,
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在点
;(3)存在点![]() ,其坐标为
,其坐标为![]() 或
或![]()
【解析】
(1)利用平移得性质确定出平移得单位和方向;
(2)根据平移得性质,设出平移单位,根据S△BCD=7(S△BCD建立方程求解,即可);
(3)设出点P的坐标,表示出PC用![]() ,建立方程求解即可.
,建立方程求解即可.
(1)∵B(3,0)平移后的对应点![]() ,
,
∴设![]() ,
,
∴![]()
即线段![]() 向左平移5个单位,再向上平移4个单位得到线段
向左平移5个单位,再向上平移4个单位得到线段![]()
∴![]() 点平移后的对应点
点平移后的对应点![]() ;
;
(2)∵点C在![]() 轴上,点D在第二象限,
轴上,点D在第二象限,
∴线段![]() 向左平移3个单位,再向上平移
向左平移3个单位,再向上平移![]() 个单位,∴
个单位,∴![]()
连接![]() ,
,
![]()
![]() ,∴
,∴![]()
∴![]() ;
;
(3)存在
设点![]() ,∴
,∴![]()
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]()
∴存在点![]() ,其坐标为
,其坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目
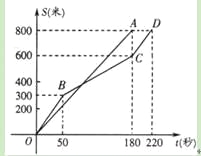
【题目】为方便市民出行,甲、乙两家公司推出专车服务,运价收费如下:设行驶路程![]() 时,用含
时,用含![]() 的代数式表示乙公司的运价.
的代数式表示乙公司的运价.
行驶路程 | 收费标准 | |
甲 | 乙 | |
不超过 | 起步价6元 | 起步价7元 |
超过 | 每公里2.1元 | 每公里1.6元 |
超出 | 每公里2.2元 | |
(1)当![]() 时,则费用表示为 元;当
时,则费用表示为 元;当![]() 时,则费用表示为 元.
时,则费用表示为 元.
(2)当行驶路程![]() 时,对于乘客来说,哪个专车更合算,为什么?
时,对于乘客来说,哪个专车更合算,为什么?
(3)当行驶路程![]() 时,对于乘客来说,哪个专车更合算,为什么?
时,对于乘客来说,哪个专车更合算,为什么?