��Ŀ����
 ��2011•����ģ�⣩����֪�����������������е���߶ν��������ε���λ�ߣ�ͨ��֤�����Եõ��������ε���λ��ƽ���������εĵ����ߣ��ҵ��ڵ����ߵ�һ�롱������������λ�ߣ����ǰ��������������е���߶ν������ε���λ�ߣ���ͼ������ABCD�У�AD��BC����E��F�ֱ���AB��CD���е㣬�۲�EF��λ�ã�������������λ�ߵ����ʣ����ܷ������ε���λ����ʲô���ʣ�֤����Ľ��ۣ�
��2011•����ģ�⣩����֪�����������������е���߶ν��������ε���λ�ߣ�ͨ��֤�����Եõ��������ε���λ��ƽ���������εĵ����ߣ��ҵ��ڵ����ߵ�һ�롱������������λ�ߣ����ǰ��������������е���߶ν������ε���λ�ߣ���ͼ������ABCD�У�AD��BC����E��F�ֱ���AB��CD���е㣬�۲�EF��λ�ã�������������λ�ߵ����ʣ����ܷ������ε���λ����ʲô���ʣ�֤����Ľ��ۣ���2�������E���߶�ABΪ
| AE |
| EB |
| 1 |
| 3 |
3.5
3.5
��ֱ����д���������3�������E���߶�ABΪ
| AE |
| EB |
| m |
| n |
��������1������AF���ӳ���BC���ӳ����ڵ�G��Ȼ�����ýDZ߽�֤����ADF���GCFȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�DF=CF��AD=CG��Ȼ���ٸ��������ε���λ�߶������ɵ�֤����
��2������A��AH��CD��EF�ڵ�G����BC�ڵ�H������ƽ���ı��εĶԱ���ȿɵ�GF=AD���ٸ���ƽ���߷��߶γɱ���������ʾ��EG�ij��ȣ�Ȼ����Ӽ������EF�ij���
��3���루2��ͬ�������EF�ij���
��2������A��AH��CD��EF�ڵ�G����BC�ڵ�H������ƽ���ı��εĶԱ���ȿɵ�GF=AD���ٸ���ƽ���߷��߶γɱ���������ʾ��EG�ij��ȣ�Ȼ����Ӽ������EF�ij���
��3���루2��ͬ�������EF�ij���
���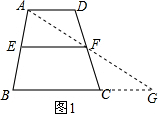 �⣺��1��֤������ͼ1������AF���ӳ���BC���ӳ����ڵ�G��
�⣺��1��֤������ͼ1������AF���ӳ���BC���ӳ����ڵ�G��
��AD��BC��
���D=��GCF��
��F��CD���е㣬
��DF=FC��
�ڡ�ADF���GCF�У�
��
���ADF�ա�GCF��ASA����
��AF=FG��AD=CG��
��EF��BC����EF=
BG��
��BG=BC+CG��
��EF=
��AD+BC����
�����ε���λ��ƽ���ڵױ߲��ҵ������͵�һ�룻
��2����ͼ2������A��AH��CD��EF�ڵ�G����BC�ڵ�H��
��AD��BC��
��GF=CH=AD��
��
=
��
��
=
=
��
��EG=
��
��EF=EG+GF=
+AD��
��AD=3��BC=5��
��EF=
+3=3.5��
��3����ͼ3������A��AH��CD��EF�ڵ�G����BC�ڵ�H��
��AD��BC��
��GF=CH=AD��
��
=
��
��
=
=
��
��EG=
BH��
��EF=EG+GF=
BH+AD��
��AD=a��BC=b��
��EF=
����b-a��+a=
��
 �⣺��1��֤������ͼ1������AF���ӳ���BC���ӳ����ڵ�G��
�⣺��1��֤������ͼ1������AF���ӳ���BC���ӳ����ڵ�G����AD��BC��
���D=��GCF��
��F��CD���е㣬
��DF=FC��
�ڡ�ADF���GCF�У�
|
���ADF�ա�GCF��ASA����
��AF=FG��AD=CG��
��EF��BC����EF=
| 1 |
| 2 |
��BG=BC+CG��
��EF=
| 1 |
| 2 |
�����ε���λ��ƽ���ڵױ߲��ҵ������͵�һ�룻
��2����ͼ2������A��AH��CD��EF�ڵ�G����BC�ڵ�H��
��AD��BC��
��GF=CH=AD��
��
| AE |
| EB |
| 1 |
| 3 |
��
| EG |
| BH |
| AE |
| AB |
| 1 |
| 4 |

��EG=
| BH |
| 4 |
��EF=EG+GF=
| BH |
| 4 |
��AD=3��BC=5��
��EF=
| 5-3 |
| 4 |
��3����ͼ3������A��AH��CD��EF�ڵ�G����BC�ڵ�H��
��AD��BC��
��GF=CH=AD��
��
| AE |
| EB |
| m |
| n |
��
| EG |
| BH |
| AE |
| AB |
| m |
| m+n |
��EG=
| m |
| m+n |
��EF=EG+GF=
| m |
| m+n |
��AD=a��BC=b��
��EF=
| m |
| m+n |
| mb+na |
| m+n |
������������Ҫ���������ε���λ����ƽ���߷��߶γɱ���������ͨ���������ߣ������ε�����ת��Ϊ�����ε���λ�߽��н���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
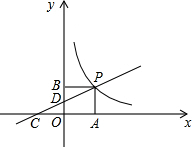 ��2011•����ģ�⣩��ͼ��һ�κ���y=kx+2��ͼ���뷴��������y=
��2011•����ģ�⣩��ͼ��һ�κ���y=kx+2��ͼ���뷴��������y=