题目内容
(本题12分)
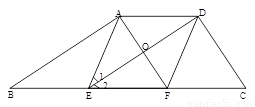
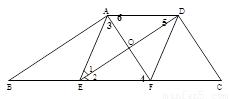
如图,AD//BC,点E、F在BC上,∠1=∠2,AF⊥DE,垂足为点O.
(1)求证:四边形AEFD是菱形;
(2)若BE=EF=FC,求∠BAD+∠ADC的度数;
(3)若BE=EF=FC,设AB = m,CD = n,求四边形ABCD的面积.
(1)( 4分)证明:
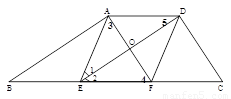
(方法一)∵AF⊥DE
∴∠1+∠3=90° 即:∠3=90°-∠1
∴∠2+∠4=90° 即:∠4=90°-∠2
又∵∠1=∠2 ∴∠3=∠4 ∴AE = EF
∵AD//BC ∴∠2=∠5
∵∠1=∠2 ∴∠1=∠5
∴AE = AD ∴EF = AD 2分
∵AD//EF
∴四边形AEFD是平行四边形 1分
又∵AE = AD
∴四边形AEFD是菱形 1分
(方法二)∵AD//BC ∴∠2=∠5
∵∠1=∠2 ∴∠1=∠5
∵AF⊥DE ∴∠AOE=∠AOD=90°
在△AEO和△ADO中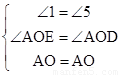 ∴△AEO
∴△AEO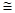 △ADO ∴EO=OD
△ADO ∴EO=OD
在△AEO和△FEO中 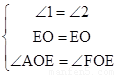 ∴△AEO
∴△AEO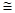 △FEO ∴AO=FO 2分
△FEO ∴AO=FO 2分
∴AF与ED互相平分 1分
∴四边形AEFD是平行四边形
又∵AF⊥DE
∴四边形AEFD是菱形 1分
(2)( 5分)
∵菱形AEFD ∴AD=EF
∵BE=EF ∴AD=BE
又∵AD//BC ∴四边形ABED是平行四边形 1分
∴AB//DE ∴∠BAF=∠EOF
同理可知 四边形AFCD是平行四边形
∴AF//DC ∴∠EDC=∠EOF
又∵AF⊥ED ∴∠EOF=∠AOD=90°
∴∠BAF=∠EDC=∠EOF=90° 2分
∴∠5 +∠6=90° 1分
∴∠BAD+∠ADC=∠BAF+∠6 +∠5+∠EDC =270° 1分
(3)( 3分)由(2)知∠BAF =90°平行四边形AFCD ∴AF=CD=n
又∵AB=m
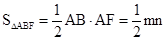 1分
1分
由(2)知 平行四边形ABED ∴DE=AB=m
由(1)知OD=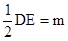
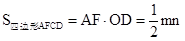 1分
1分
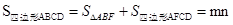 1分
1分
【解析】略





 x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y=