题目内容
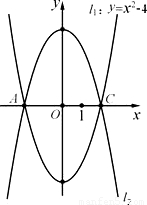
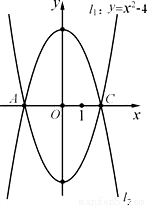
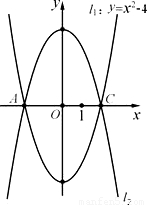
(2006•资阳)如图,已知抛物线l1:y=x2-4的图象与x轴相交于A、C两点,B是抛物线l1上的动点(B不与A、C重合),抛物线l2与l1关于x轴对称,以AC为对角线的平行四边形ABCD的第四个顶点为D.(1)求l2的解析式;
(2)求证:点D一定在l2上;
(3)?ABCD能否为矩形?如果能为矩形,求这些矩形公共部分的面积(若只有一个矩形符合条件,则求此矩形的面积);如果不能为矩形,请说明理由.
注:计算结果不取近似值.
【答案】分析:(1)根据l1的解析式可求l1与x轴的交点为A(-2,0),C(2,0),顶点坐标是(0,-4),l2与l1关于x轴对称,实际上是l2与l1的顶点关于x轴对称,即l2的顶点为(0,4),设顶点式,可求抛物线l2的解析式;
(2)平行四边形是中心对称图形,A、C关于原点对称,则B、D也关于原点对称,设点B(m,n),则点D(-m,-n),由于B(m,n)点是y=x2-4上任意一点,则n=m2-4,∴-n=-(m2-4)=-m2+4=-(-m)2+4,可知点D(-m,-n)在l2y=-x2+4的图象上;
(3)构造∠ABC=90°是关键,连接OB,只要证明OB=OC即可,为求OB长,过点B作BH⊥x轴于H,用B的坐标为(x,x2-4),可求OB,用OB=OC求x,再计算面积.
解答:解:(1)设l2的解析式为y=ax2+bx+c(a≠0),
∵l1与x轴的交点为A(-2,0),C(2,0),顶点坐标是(0,-4),l2与l1关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4),(1分)
∴ (2分)
(2分)
∴a=-1,b=0,c=4,
即l2的解析式为y=-x2+4.(3分)
(还可利用顶点式、对称性关系等方法解答)
(2)设点B(m,n)为l1:y=x2-4上任意一点,则n=m2-4,(*)
∵四边形ABCD′是平行四边形,点A、C关于原点O对称,
∴B、D′关于原点O对称,(4分)
∴点D′的坐标为D′(-m,-n).
由式方程式可知,-n=-(m2-4)=-(-m)2+4,
即点D′的坐标满足y=-x2+4,又D与D′关于y轴对称,
∴点D在l2上.(5分)
(3)?ABCD能为矩形.(6分)
过点B作BH⊥x轴于H,由点B在l1:y=x2-4上,可设点B的坐标为(x,x2-4),
则OH=|x|,BH=|x2-4|.
易知,当且仅当BO=AO=2时,?ABCD为矩形.
在Rt△OBH中,由勾股定理得,|x|2+|x2-4|2=22,
(x2-4)(x2-3)=0,
∴x=±2(舍去)、x=±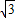 .(7分)
.(7分)
所以,当点B坐标为B(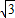 ,-1)或B′(-
,-1)或B′(-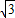 ,-1)时,?ABCD为矩形,
,-1)时,?ABCD为矩形,
此时,点D的坐标分别是D(-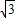 ,1)、D′(
,1)、D′( ,1).
,1).
因此,符合条件的矩形有且只有2个,即矩形ABCD和矩形AB′CD′.(8分)
设直线AB与y轴交于E,显然,△AOE∽△AHB,
∴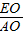 =
=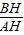 ,
,
∴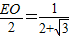 .
.
∴EO=4-2 .(9分)
.(9分)
由该图形的对称性知矩形ABCD与矩形AB′CD′重合部分是菱形,其面积为
S=2S△ACE=2× ×AC×EO=2×
×AC×EO=2× ×4×(4-2
×4×(4-2 )=16-8
)=16-8 .(10分)
.(10分)
(还可求出直线AB与y轴交点E的坐标解答)
点评:本题是一道函数型综合题,涉及二次函数、相似形、四边形等知识,三个小题的坡度设计很恰当,能较好地体现出试题的区分度,对第2题的证明过程要仔细领悟.
(2)平行四边形是中心对称图形,A、C关于原点对称,则B、D也关于原点对称,设点B(m,n),则点D(-m,-n),由于B(m,n)点是y=x2-4上任意一点,则n=m2-4,∴-n=-(m2-4)=-m2+4=-(-m)2+4,可知点D(-m,-n)在l2y=-x2+4的图象上;
(3)构造∠ABC=90°是关键,连接OB,只要证明OB=OC即可,为求OB长,过点B作BH⊥x轴于H,用B的坐标为(x,x2-4),可求OB,用OB=OC求x,再计算面积.
解答:解:(1)设l2的解析式为y=ax2+bx+c(a≠0),
∵l1与x轴的交点为A(-2,0),C(2,0),顶点坐标是(0,-4),l2与l1关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4),(1分)

∴
 (2分)
(2分)∴a=-1,b=0,c=4,
即l2的解析式为y=-x2+4.(3分)
(还可利用顶点式、对称性关系等方法解答)
(2)设点B(m,n)为l1:y=x2-4上任意一点,则n=m2-4,(*)
∵四边形ABCD′是平行四边形,点A、C关于原点O对称,
∴B、D′关于原点O对称,(4分)
∴点D′的坐标为D′(-m,-n).
由式方程式可知,-n=-(m2-4)=-(-m)2+4,
即点D′的坐标满足y=-x2+4,又D与D′关于y轴对称,
∴点D在l2上.(5分)
(3)?ABCD能为矩形.(6分)
过点B作BH⊥x轴于H,由点B在l1:y=x2-4上,可设点B的坐标为(x,x2-4),
则OH=|x|,BH=|x2-4|.
易知,当且仅当BO=AO=2时,?ABCD为矩形.
在Rt△OBH中,由勾股定理得,|x|2+|x2-4|2=22,
(x2-4)(x2-3)=0,
∴x=±2(舍去)、x=±
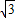 .(7分)
.(7分)所以,当点B坐标为B(
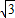 ,-1)或B′(-
,-1)或B′(-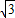 ,-1)时,?ABCD为矩形,
,-1)时,?ABCD为矩形,此时,点D的坐标分别是D(-
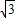 ,1)、D′(
,1)、D′( ,1).
,1).因此,符合条件的矩形有且只有2个,即矩形ABCD和矩形AB′CD′.(8分)
设直线AB与y轴交于E,显然,△AOE∽△AHB,
∴
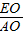 =
=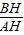 ,
,∴
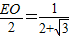 .
.∴EO=4-2
 .(9分)
.(9分)由该图形的对称性知矩形ABCD与矩形AB′CD′重合部分是菱形,其面积为
S=2S△ACE=2×
 ×AC×EO=2×
×AC×EO=2× ×4×(4-2
×4×(4-2 )=16-8
)=16-8 .(10分)
.(10分)(还可求出直线AB与y轴交点E的坐标解答)
点评:本题是一道函数型综合题,涉及二次函数、相似形、四边形等知识,三个小题的坡度设计很恰当,能较好地体现出试题的区分度,对第2题的证明过程要仔细领悟.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目