题目内容
如图,点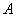 在抛物线
在抛物线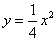 上,过点
上,过点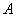 作与
作与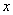 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长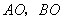 分别与抛物线
分别与抛物线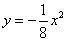 相交于点
相交于点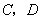 ,连接
,连接 ,设点
,设点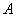 的横坐标为
的横坐标为 ,且
,且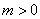 .
.
(1).当 时,求点
时,求点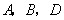 的坐标;
的坐标;
(2).当 为何值时,四边形
为何值时,四边形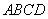 的两条对角线互相垂直;
的两条对角线互相垂直;
(3).猜想线段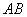 与
与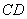 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
解:(1) 点
点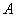 在抛物线
在抛物线 上,且
上,且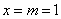 ,
, ,······························ 1分
,······························ 1分
 点
点 与点
与点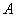 关于
关于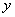 轴对称,
轴对称,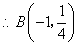 .························································ 2分
.························································ 2分
设直线 的解析式为
的解析式为 ,
,
 .······················································································· 3分
.······················································································· 3分
解方程组 ,得
,得 .································································· 4分
.································································· 4分
(2)当四边形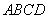 的两对角线互相垂直时,由对称性得直线
的两对角线互相垂直时,由对称性得直线 与
与 轴的夹角等于
轴的夹角等于 所以点
所以点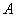 的横、纵坐标相等, 5分
的横、纵坐标相等, 5分
这时,设 ,代入
,代入 ,得
,得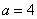 ,
, .
.
即当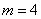 时,四边形
时,四边形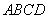 的两条对角线互相垂直.········································· 6分
的两条对角线互相垂直.········································· 6分
(3)线段 .········································································································ 7分
.········································································································ 7分
 点
点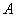 在抛物线
在抛物线 ,且
,且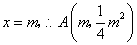 ,
,
得直线 的解析式为
的解析式为 ,
,
解方程组 ,得点
,得点 ······················································· 8分
······················································· 8分
由对称性得点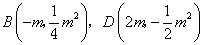 ,··················································· 9分
,··················································· 9分
 ,
,
 .
10分
.
10分
【解析】略

 阅读快车系列答案
阅读快车系列答案 在抛物线
在抛物线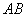 与
与
 在抛物线
在抛物线 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长 分别与抛物线
分别与抛物线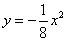 相交于点
相交于点 ,连接
,连接 ,设点
,设点 ,且
,且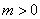 .
.
 时,求点
时,求点 的坐标;
的坐标; 的两条对角线互相垂直;
的两条对角线互相垂直; 与
与 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论. 在抛物线
在抛物线 上,过点
上,过点 轴平行的直线交抛物线于点
轴平行的直线交抛物线于点 ,延长
,延长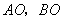 分别与抛物线
分别与抛物线 相交于点
相交于点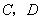 ,连接
,连接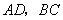 ,设点
,设点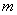 ,且
,且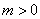 .
.
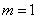 时,求点
时,求点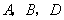 的坐标;
的坐标;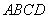 的两条对角线互相垂直;
的两条对角线互相垂直;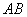 与
与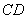 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.