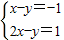题目内容
（2007•聊城）美丽的东昌湖赋予江北水城以灵性，周边景点密布．如图，A、B为湖滨的两个景点，C为湖心的一个景点，景点B在景点C的正东，从景点A看，景点B在北偏东75°方向，景点C在北偏东30°方向，一游客自景点A驾船以每分钟20米的速度行驶了10分钟到达景点C，之后又以同样的速度驶向景点B，该游客从景点C到景点B需用多长时间？（精确到1分钟）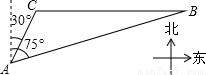
【答案】分析：过点A作AD垂直于直线BC，垂足为D，在Rt△ADC中，满足解直角三角形的条件，可以求出AD、DC．在Rt△ADB中，根据解直角三角形的条件求出CB，进而求出时间．
解答：解：如图，过点A作AD垂直于直线BC，垂足为D，
根据题意，得AC=20×10=200．
在Rt△ADC中，
AD=AC•cos∠CAD=200•cos30°=100
，
DC=AC•sin∠CAD=200•sin30°=100．
在Rt△ADB中，
DB=AD•tan∠BAD=100
tan75°．
∴CB=DB-DC=100
tan75°-100．
∴
=5
tan75°-5≈27．
即该游客自景点C驶向景点B约需27分钟．
点评：解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
解答：解：如图，过点A作AD垂直于直线BC，垂足为D，
根据题意，得AC=20×10=200．
在Rt△ADC中，
AD=AC•cos∠CAD=200•cos30°=100
，DC=AC•sin∠CAD=200•sin30°=100．
在Rt△ADB中，
DB=AD•tan∠BAD=100
tan75°．∴CB=DB-DC=100
tan75°-100．∴
=5tan75°-5≈27．即该游客自景点C驶向景点B约需27分钟．
点评：解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
相关题目
