Question

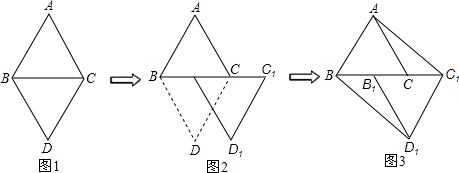
下列图中，已知等边△ABC和等边△DBC有公共的底边BC



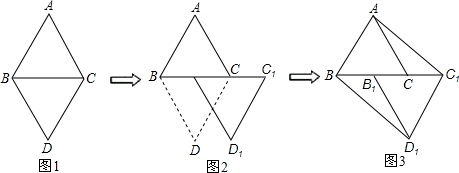
（1）以图（1）中的某个点为旋转中心，旋转△DBC与△ABC重合，则旋转中心为______（写出所有满足条件的点）
（2）如图（2），已知B₁是BC的中点，现沿着由B到B₁的方向，将△DBC平移到△D₁B₁C₁的位置，连接AC₁，BD₁得到的四边形ABD₁C₁是什么特殊四边形？说明你的理由．
（3）在四边形ABD₁C₁中有______对全等三角形，请你选出其中一对进行证明．

Answer 1

（1）∵等边△ABC和等边△DBC有公共的底边BC，
∴AB=BC=CD=AD，
∴四边形ABCD是菱形．
∴要旋转△DBC，使△DBC与△ABC重合，有三点分别为：B点、C点、BC的中点；

（2）图中有3对全等三角形，
据平移的性质，得到BB₁=CC₁，
根据等边三角形的性质，得到AC=B₁D₁，∠BB₁D₁=∠ACC₁，
∴△BB₁D₁≌△ACC₁；

（3）四边形ABD₁C₁是平行四边形．理由如下：
据平移的性质，得到BB₁=CC₁，
根据等边三角形的性质，得到AC=B₁D₁，∠BB₁D₁=∠ACC₁，
∴△BB₁D₁≌△ACC₁，
∴AC₁=BD₁，
又AB=C₁D₁，
∴四边形ABD₁C₁是平行四边形．
故答案为B点、C点、BC的中点，3．