题目内容
5、如果a,b是整数,x2-x-1是ax3+bx2+1的一个因式,那么a等于( )
分析:将x2-x-1看成整体,对代数式ax3+bx2+1配项使其满足x2-x-1是ax3+bx2+1的一个因式,得出关于a的方程解出a的值即可.
解答:解:∵ax3+bx2+1,
=ax(x2-x-1)+ax2+ax+bx2+1,
=ax(x2-x-1)+(a+b)(x2-x-1)+ax+1+(a+b)(x+1),
又∵x2-x-1是ax3+bx2+1的一个因式,
∴ax+1+(a+b)(x+1)=0,
即(2a+b)x+a+b+1=0,
∴2a+b=0,a+b+1=0,
解得a=1.
故选D.
=ax(x2-x-1)+ax2+ax+bx2+1,
=ax(x2-x-1)+(a+b)(x2-x-1)+ax+1+(a+b)(x+1),
又∵x2-x-1是ax3+bx2+1的一个因式,
∴ax+1+(a+b)(x+1)=0,
即(2a+b)x+a+b+1=0,
∴2a+b=0,a+b+1=0,
解得a=1.
故选D.
点评:本题考查因式分解的运用,注意运用整体代入法求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
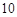 元钱买一包牛奶钱不足,打九折后钱又有剩余,如果牛奶的标价是整数元,那么标价是__________元.
元钱买一包牛奶钱不足,打九折后钱又有剩余,如果牛奶的标价是整数元,那么标价是__________元.