题目内容
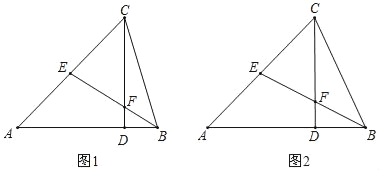
【题目】如图，△ABC中，∠A＝45°，过点C作CD⊥AB于点D，E为AC的中点，连接EB，交CD于点F．
（1）如图1，若∠EBA＝30°，EB＝2，求AE的长：
（2）如图2，若F恰好为EB的中点，求证：CF＝DF+
AD．
【答案】（1）AE＝
；（2）证明见解析.
【解析】
（1）先过E作垂线，构建直角三角形求AE（2）F是EB的中点，据此找到边与边的关系，利用等量代换思想证明出CF＝DF+
AD
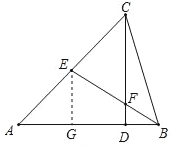
（1）过E作EG⊥AB于G，
∴∠AGE＝∠BGE＝90°，
∵∠EBA＝30°，EB＝2，
∴EG＝BE＝1，
∵∠A＝45°，
∴AG＝EG＝1，
∴AE＝；
（2）证明：过E作EG⊥AB于G，
∵CD⊥AB，
∴EG∥CD，
∵E为AC的中点，
∴EG＝CD，
∵F恰好为EB的中点，
∴DF＝EG＝
CD，
∴CF＝
CD，
∵∠A＝45°，
∴CD＝AD，
∴CF＝AD，
∵DF+AD＝CD+AD＝AD+AD＝AD，
∴CF＝DF+AD．
练习册系列答案
阅读快车系列答案
相关题目
