题目内容
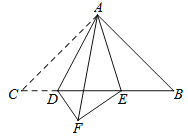
【题目】已知:如图,△ABC 中,∠CAB=90°,AC=AB,点 D、E 是 BC 上的两点,且∠DAE=45°,△ADC 与△ADF 关于直线AD 对称.
(1)求证:△AEF≌△AEB;
(2)求∠DFE 的度数.
【答案】(1)详见解析;(2)90°.
【解析】
(1)根据折叠的性质得到△ADF≌△ADC,根据全等三角形的性质得到AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD,由于AB=AC,于是得到AF=AB,证得∠FAE=∠BAE,即可得到结论;
(2)由(1)知△AFE≌△ABE,根据全等三角形的性质得到∠AFE=∠B,即可得到结论.
(1)∵把△ADC沿着AD折叠,得到△ADF,∴△ADF≌△ADC;
∴AC=AF,CD=FD,∠C=∠DFA,∠CAD=∠FAD.
∵AB=AC,∴AF=AB.
∵∠DAE=45°,∴∠CAD+∠BAE=45°.
∵∠CAD=∠FAD,∴∠FAE=∠BAE.
在△AFE与△ABE中,∵ ,∴△AEF≌△AEB;
,∴△AEF≌△AEB;
(2)由(1)知△AEF≌△AEB,∴∠AFE=∠B.
∵∠C=∠DFA,∴∠DFE=∠DFA+∠EFA=∠B+∠C=90°.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往B地,如表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
行驶时间x/时 | 0 | 1 | 2 | 2.5 |
余油量y/升 | 100 | 80 | 60 | 50 |
则y与x的函数关系式为_____,自变量x的取值范围为_____.
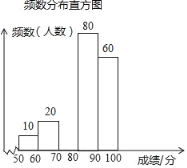
【题目】某校组织了全校1500名学生参加传统文化知识网络竞赛.赛后随机抽取了其中200名学生的成绩作为样本进行整理,并制作了如下不完整的频数分布表和频数分布直方图.
成绩(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | n |
70≤x<80 | m | 0.15 |
80≤x<90 | 80 | 0.40 |
90≤x<100 | 60 | 0.30 |
请根据图表提供的信息,解答下列各题:
(1)表中m= ,n= ,请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段80≤x<90对应扇形的圆心角的度数是 ;
(3)若成绩在80分以上(包括80分)为合格,则参加这次竞赛的1500名学生中成绩合格的大约有多少名?