题目内容
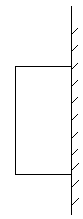
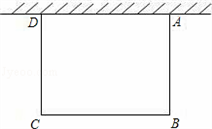
 如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为
如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为
- A.10米
- B.15米
- C.20米
- D.25米
A
分析:本题考查二次函数最小(大)值的求法.
解答:设矩形ABCD的边AB为x米,则宽为40-2x,
S=(40-2x)x=-2x2+40x.
要使矩形ABCD面积最大,
则x=- =-
=-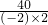 =10m,
=10m,
即x的长为10m.
故选A.
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a的绝对值是较小的整数时,用配方法较好,如y=-x2-2x+5,y=3x2-6x+1等用配方法求解比较简单.
分析:本题考查二次函数最小(大)值的求法.
解答:设矩形ABCD的边AB为x米,则宽为40-2x,
S=(40-2x)x=-2x2+40x.
要使矩形ABCD面积最大,
则x=-
 =-
=-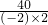 =10m,
=10m,即x的长为10m.
故选A.
点评:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a的绝对值是较小的整数时,用配方法较好,如y=-x2-2x+5,y=3x2-6x+1等用配方法求解比较简单.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
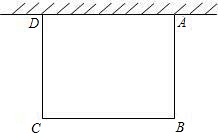 如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )| A、10米 | B、15米 | C、20米 | D、25米 |