题目内容
(本小题满分12分)
如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当 时,求线段
时,求线段 的长;
的长;
(2)点M在线段AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形,若可以,请直接写出t的值(不需解题步骤);若不可以,请说明理由.
(3)若△PCQ的面积为y,请求y关于出t 的函数关系式及自变量的取值范围;
解:(1)由Rt△AQM∽Rt△CAD. ……………………………………………2分
∴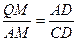 . 即
. 即 ,∴
,∴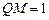 . …………………………………1分
. …………………………………1分
(2)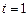 或
或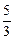 或4. ……………………………………………3分
或4. ……………………………………………3分
(3)当0<t<2时,点P在线段CD上,设直线l交CD于点E
由(1)可得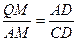 . 即QM=2t.∴QE=4-2t.………………………2分
. 即QM=2t.∴QE=4-2t.………………………2分
∴S△PQC =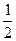 PC·QE=
PC·QE= ………………………………………………1分
………………………………………………1分
即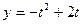
当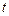 >2时,过点C作CF⊥AB交AB于点F,交PQ于点H.
>2时,过点C作CF⊥AB交AB于点F,交PQ于点H.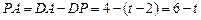 .
.
由题意得,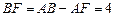 .
.
∴ 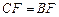 . ∴
. ∴ .
.
∴ 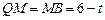 . ∴
. ∴ .
.
∴ 四边形AMQP为矩形.
∴ PQ∥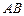 .CH⊥PQ,HF="AP=6-" t
.CH⊥PQ,HF="AP=6-" t
∴ CH="AD=HF=" t-2 …………………………………………………………1分
∴S△PQC =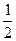 PQ·CH=
PQ·CH=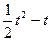 ………………………………………1分
………………………………………1分
即y=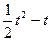
综上所述 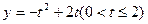 或y=
或y=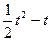 ( 2<
( 2<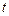 <6) …………………1分
<6) …………………1分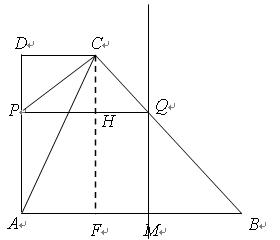
解析

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题:


 同侧,在直线
同侧,在直线 ,连接
,连接 ,与直线
,与直线


