题目内容
我县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产。他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材。如图所示,(单位:cm


甲
(1)列出方程(组),求出图甲中a与b的值。
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙的竖式与横式两种无盖礼品盒。
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:

③做成的竖式和横式两种无盖礼品盒总数最多是 个;此时,横式无盖礼品盒可以做 个。(在横线上直接写出答案,无需书写过程)


甲
(1)列出方程(组),求出图甲中a与b的值。
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙的竖式与横式两种无盖礼品盒。
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:

 | 竖式无盖(个) | 横式无盖(个) |
| x | y | |
| A型(张) | 4x | 3y |
| B型(张) | x | |
(1)a=60,b=40(2)① 64,38 ② 2y ③ 20;16或17或18
试题分析:(1)解:由题意得:
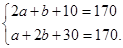
解得
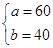
(2)30张标准板材用裁法一裁剪可得30×2=60张A型。和30张B型。
4张标准板材用裁法二裁剪则得到4张A型和4×2=8张B型。
则共产生A型60+4=64(张);产生B型30+8=38(张)。
 | 竖式无盖(个) | 横式无盖(个) |
| x | y | |
| A型(张) | 4x | 3y |
| B型(张) | x | |
则做两款盒子共需要A型4x+3y张,B型x+2y张。
则4x+3y≤64;x+2y≤38.两式相加得5x+5y≤102.则x+y≤20.4.所以最多做20个。
两式相减得3x+y≤26.则2x≤5.6,解得x≤2.8,x≈2(个).则y≤18.
则横式约可做18个。
点评:本题难度较大,主要考查学生对二元一次方程组解决生产问题实际应用。要求学生培养数形结合思想,并运用到日常生活和学习考试中去。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

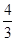 倍
倍 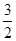 倍
倍 倍
倍  倍
倍 写成用含x的代数式表示y的形式是
写成用含x的代数式表示y的形式是 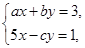 甲正确地解得
甲正确地解得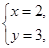 ,而乙粗心地把c看错了,解得
,而乙粗心地把c看错了,解得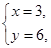 ,则a = ,b = ,c = .
,则a = ,b = ,c = .

 的解是( )
的解是( )



