题目内容
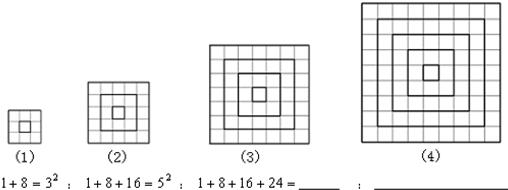
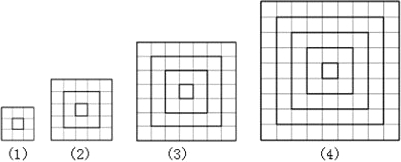
观察下列图形及图形所对应的等式,探究其中的规律:
1+8=32;1+8+16=52;1+8+16+24=;.
(1)在横线上写出第3个图形所对应的算式的结果;
(2)在横线上写出第4个图形所对应的等式;
(3)根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为(用含n的代数式表示).
解:(1)1+8+16+24=72;
(2)∵第1个图形是:1+8=32,第2个图形是:1+8+16=52,
第3个图形是:1+8+16+24=72
由1,2,3得:分别是3,5,7的平方,可得出第4个是9的平方;
(3)∵由(2)中分析可知,3,5,7,9…第n个的表示方法为:
2n+1,1+8+16+24+…+8n(n是正整数)=(2n+1)2.
分析:由已知条件1+8×1=32;1+8×1+8×2=52,直接求出1+8+8×2+8×3=72,由1+8=32;1+8+8×2=52,1+8+8×2+8×3=72可以发现出第4个是9的平方,进而求出1+8+16+24+…+8n(n是正整数)的结果.
点评:此题主要考查了数的规律性注意由已知发现数字的变化,从而得出一般规律.
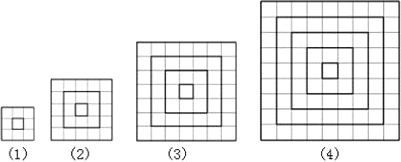
(2)∵第1个图形是:1+8=32,第2个图形是:1+8+16=52,
第3个图形是:1+8+16+24=72
由1,2,3得:分别是3,5,7的平方,可得出第4个是9的平方;
(3)∵由(2)中分析可知,3,5,7,9…第n个的表示方法为:
2n+1,1+8+16+24+…+8n(n是正整数)=(2n+1)2.
分析:由已知条件1+8×1=32;1+8×1+8×2=52,直接求出1+8+8×2+8×3=72,由1+8=32;1+8+8×2=52,1+8+8×2+8×3=72可以发现出第4个是9的平方,进而求出1+8+16+24+…+8n(n是正整数)的结果.
点评:此题主要考查了数的规律性注意由已知发现数字的变化,从而得出一般规律.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目