题目内容
【题目】2018长春国际马拉松赛于2018年5月27日在长春市举行,其中10公里跑起点是长春体育中心,终点是卫星广场.比赛当天赛道上距离起点5km处设置一个饮料站,距离起点7.5km处设置一个食品补给站.小明报名参加了10公里跑项目.为了更好的完成比赛,小明在比赛前进行了一次模拟跑,从起点出发,沿赛道跑向终点,小明匀速跑完前半程后,将速度提高了![]() ,继续匀速跑完后半程.小明与终点之间的路程
,继续匀速跑完后半程.小明与终点之间的路程![]() 与时间
与时间![]() 之间的函数图象如图所示,根据图中信息,完成以下问题.(1公里=1千米)
之间的函数图象如图所示,根据图中信息,完成以下问题.(1公里=1千米)
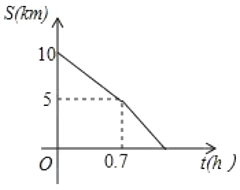
(1)小明从起点匀速跑到饮料站的速度为_______![]() ,小明跑完全程所用时间为________
,小明跑完全程所用时间为________![]() ;
;
(2)求小明从饮料站跑到终点的过程中![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)求小明从起点跑到食品补给站所用时间.
【答案】(1)![]() ,1.2;(2)S=﹣10t+12(0.7≤t≤1.2);(3)0.95
,1.2;(2)S=﹣10t+12(0.7≤t≤1.2);(3)0.95
【解析】
(1)根据图象可知小明从起点匀速跑到饮料站用时0.7小时,根据“速度=路程÷时间”即可解答;
(2)根据题意和函数图象中的数据可以求得小明从饮料站跑到终点的过程中S与t之间的函数表达式;
(3)根据题意,可以列出关于a的不等式,从而可以求得a的取值范围,本题得以解决.
解:(1)小明从起点匀速跑到饮料站的速度为:![]() km/h,小明跑完全程所用时间为:
km/h,小明跑完全程所用时间为:![]() (小时);
(小时);
故答案为:![]() ;1.2;
;1.2;
(2)设明张从饮料站跑到终点的过程中S与t之间的函数表达式为S=kt+b,
![]() ,解得
,解得![]() ,
,
即小明从饮料站跑到终点的过程中S与t之间的函数表达式为S=﹣10t+12(0.7≤t≤1.2);
(3)10﹣7.5=2.5,
∴将S=2.5代入S=﹣10t+12,得
2.5=﹣10t+12,得t=0.95,
答:小明从起点跑到食品补给站所用的时间为0.95小时.

 轻松课堂单元期中期末专题冲刺100分系列答案
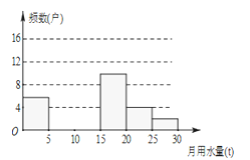
轻松课堂单元期中期末专题冲刺100分系列答案【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | m | 0.24 |
10<x≤15 | 16 | 0.32 |
15<x≤20 | 10 | 0.20 |
20<x≤25 | 4 | n |
60≤x<70 | 2 | 0.04 |
请解答以下问题:
(1)求出吗、M,n的值,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?