题目内容
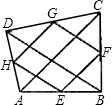 如图,任意四边形ABCD各边中点分别是E,F,G,H,若对角线AC,BD的长都为20cm,则四边形EFGH的周长是( )
如图,任意四边形ABCD各边中点分别是E,F,G,H,若对角线AC,BD的长都为20cm,则四边形EFGH的周长是( )| A、80cm | B、40cm | C、20cm | D、10cm |
分析:利用三角形中位线定理易得所求四边形的各边长都等于AC,或BD的一半,进而求四边形周长即可.
解答:解:∵E,F,G,H,是四边形ABCD各边中点
∴HG=
AC,EF=
AC,GF=HE=
BD
∴四边形EFGH的周长是HG+EF+GF+HE=
(AC+AC+BD+BD)=
×(20+20+20+20)=40cm
故选B.
∴HG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形EFGH的周长是HG+EF+GF+HE=
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查了三角形的中位线定理,解决本题的关键是找到四边形的四条边与已知的两条对角线的关系.三角形中位线的性质为我们证明两直线平行,两条线段之间的数量关系又提供了一个重要的依据.

练习册系列答案
相关题目
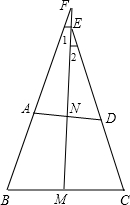 如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.
如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.
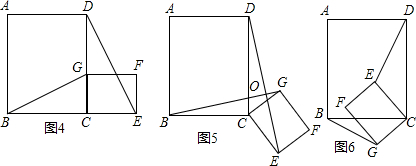
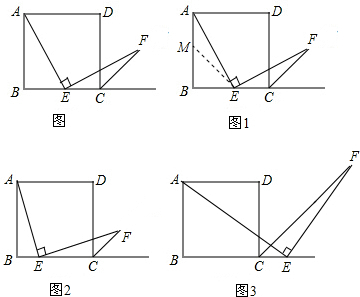
 如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.
如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.