Question

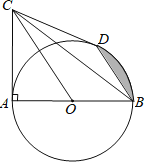
【题目】如图，在△ABC中，∠ABC＝90°，以AB的中点O为圆心，OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．

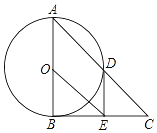
（1）判断DE与⊙O的位置关系，并说明理由；

（2）若cos∠BAD＝，BE＝12，求OE的长；

（3）求证：BC2＝2CDOE．

Answer 1

【答案】（1）DE与⊙O相切（2）15（3）证明见解析

【解析】

（1）DE与⊙O相切，连接OD，BD．证明DE⊥OD即可证明DE为⊙O的切线；

（2）由cos∠BAD=得到sin∠BAC=，又BE=12，BC=24，所以AC=30，又AC=2OE，所以OE=AC=×30=15；

（3）OE是△ABC的中位线，所以AC=2OE，证明△ABC∽△BDC，则即BC2=ACCD=2CDOE．

（1）DE与相切

理由如下：连接 OD,BD.

∵AB为直径，

∴∠ADB=90°，

在Rt△BDC中，E为斜边BC的中点，

∴CE=DE=BE= BC，

∴∠C=∠CDE，

∵OA=OD，

∴∠A=∠ADO，

∵∠ABC=90°，即∠C+∠A=90°，

∴∠ADO+∠CDE=90°，即∠ODE=90°，

∴DE⊥OD，又OD为圆的半径，

∴DE为的切线；

（2）∵cos∠BAD=

∴sin∠BAC=

又∵BE=12，E是BC的中点，即BC=24，

∴AC=30，

又∵AC=2OE，

∴OE=AC=×30=15；

（3）证明：∵E是BC的中点，O点是AB的中点，

∴OE是△ABC的中位线，

∴AC=2OE，

∵∠C=∠C，∠ABC=∠BDC，

∴△ABC∽△BDC，

∴

即BC2=ACCD．

∴BC2=2CDOE