题目内容
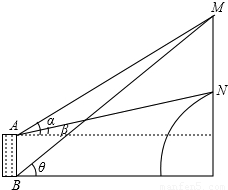
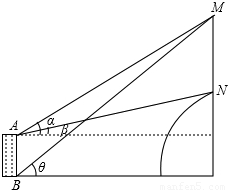
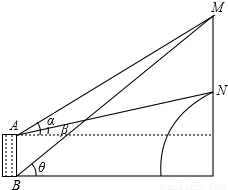
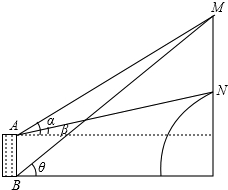某乡镇中学教学楼对面是一座小山，去年“联通”公司在山顶上建了座通讯铁塔．甲、乙两位同学想测出铁塔的高度，他们用测角器作了如下操作：甲在教学楼顶A处测得塔尖M的仰角为α，塔座N的仰角为β；乙在一楼B处只能望到塔尖M，测得仰角为θ（望不到底座），他们知道楼高AB=20m，通过查表得：tanα=0.5723，tanβ=0.2191，tanθ=0.7489；请你根据这几个数据，结合图形推算出铁塔高度MN的值．
分析：构造所给的三个角所在的直角三角形，利用相等的线段及相应的三角函数表示出MN，MD，ME，进而用MD，ME表示出楼高AB，求得相等的线段的长度，进而求得塔高即可．
解答：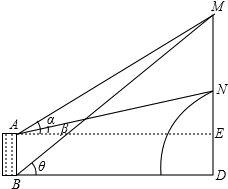
解：如图，设地平线BD，水平线AE分别交直线MN与D，E．
显然AE=BD，不妨设为m，则在Rt△AEM中，ME=mtanα．
在Rt△AEN中，NE=mtanβ，
∴MN=m（tanα-tanβ）．
在Rt△BDM中，MD=mtanθ，
而AB=DE=MD-ME=m（tanθ-tanα），
∴m=
，
∴MN=
．
∵AB=20，tanα=0.5723，tanβ=0.2191 tanθ=0.7489，
∴MN=
≈40（m）．
∴可测得铁塔的高度MN=40m．
解：如图，设地平线BD，水平线AE分别交直线MN与D，E．显然AE=BD，不妨设为m，则在Rt△AEM中，ME=mtanα．
在Rt△AEN中，NE=mtanβ，
∴MN=m（tanα-tanβ）．
在Rt△BDM中，MD=mtanθ，
而AB=DE=MD-ME=m（tanθ-tanα），
∴m=
| AB |
| tanθ-tanα |
∴MN=
| AB(tanα-tanβ) |
| tanθ-tanα |
∵AB=20，tanα=0.5723，tanβ=0.2191 tanθ=0.7489，
∴MN=
| 20×(0.5723-0.2191) |
| 0.7489-0.5723 |
∴可测得铁塔的高度MN=40m．
点评：解决本题的难点是构造所给角所在的直角三角形，关键是利用相等的线段表示出已知线段的长度．
练习册系列答案
ABC考王全优卷系列答案
相关题目
某乡镇中学教学楼对面是一座小山，去年“联通”公司在山顶上建了座通讯铁塔．甲、乙两位同学想测出铁塔的高度，他们用测角器作了如下操作：甲在教学楼顶A处测得塔尖M的仰角为α，塔座N的仰角为β；乙在一楼B处只能望到塔尖M，测得仰角为θ（望不到底座），他们知道楼高AB=20m，通过查表得：tanα=0.5723，tanβ=0.2191，tanθ=0.7489；请你根据这几个数据，结合图形推算出铁塔高度MN的值．
